Дано: y(x) = √(-x²+12*x-6)
Найти: Значения Х при минимальных значениях y(x).
1. Функция y(x) = √f(x) - существует при f(x) ≥ 0.
2. Находим точки f(x)=0 - под знаком радикала.
Решение.
1) f(x) = - x² + 12*x - 6 - функция под знаком корня.
2) Решаем квадратное уравнение f(x) = 0, находим дискриминант и корни уравнения.
D = 12² - 4*(-1)*(-6) = 144-24 = 120 - дискриминант.
√D = √120 = √(2²*30) = 2√30.
x₁ = 6 - √30, x₂ = 6 + √30 - корни квадратного уравнения. Получили область определения функции y(x):
X∈[x₁;x₂] - ООФ y(x). Минимальные значения функция на границах отрезка.
Ymin(x)=0 при x₁ = 6 - √30, x₂ = 6 + √30 - ответ.
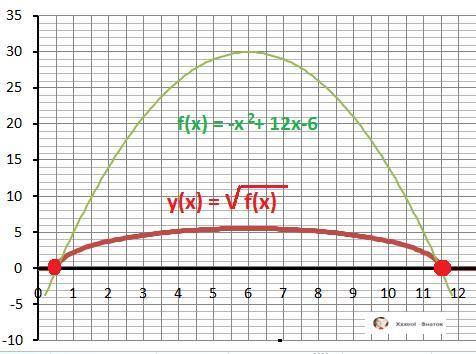
Дополнительно - графики функций - в приложении.
Максимальное значение функции y(x) равно:
Ymax(6) = √30 (≈ 5,48).
Дано: y(x) = √(-x²+12*x-6)
Найти: Значения Х при минимальных значениях y(x).
1. Функция y(x) = √f(x) - существует при f(x) ≥ 0.
2. Находим точки f(x)=0 - под знаком радикала.
Решение.
1) f(x) = - x² + 12*x - 6 - функция под знаком корня.
2) Решаем квадратное уравнение f(x) = 0, находим дискриминант и корни уравнения.
D = 12² - 4*(-1)*(-6) = 144-24 = 120 - дискриминант.
√D = √120 = √(2²*30) = 2√30.
x₁ = 6 - √30, x₂ = 6 + √30 - корни квадратного уравнения. Получили область определения функции y(x):
X∈[x₁;x₂] - ООФ y(x). Минимальные значения функция на границах отрезка.
Ymin(x)=0 при x₁ = 6 - √30, x₂ = 6 + √30 - ответ.
Дополнительно - графики функций - в приложении.
Максимальное значение функции y(x) равно:
Ymax(6) = √30 (≈ 5,48).

2. -8,6 < -8,4.
3. 0 < 5,1.
4. -3,2 < 0.
5. -0,198 > -0,2.
6. -1 5/7= -1 45/63,
-1 7/9= -1 49/63.
-1 45/63 > -1 49/63,
-1 5/7 > -1 7/9