1) Сумма корней уравнения равна
43
, а произведение корней равно
83
.
2) Сумма корней уравнения равна
-11
, а произведение корней равно
-231
.
3) Сумма корней уравнения равна
0
, а произведение корней равно
-10
.
4) Сумма корней уравнения равна
-55
, а произведение корней равно
0
.
5) Сумма корней уравнения равна
8.5
, а произведение корней равно
16
.
6) Сумма корней уравнения равна
7
, а произведение корней равно
3.8
.
Сбросить ответы Сохранить и перейти к следующему
Пошаговое объяснение:
400
Пошаговое объяснение:
Требуется вычислить сумму
S = 1 + 3 + 5 + ... + 35 + 37 + 39
Количество слагаемых равно (39-1):2+1=38:2+1=19+1=20.
Первый член арифметической прогрессии a₁=1, разность d=2. Нужно вычислить сумму первых n=20 членов прогрессии. Так как последний член прогрессии a₂₀=39, то можно использовать формулу
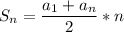 .
.
Тогда
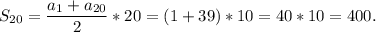
Перепишем сумму в двух видах
S = 1 + 3 + 5 + ... + 35 + 37 + 39
S = 39 + 37 + 35 + ... + 5 + 3 + 1
Так как количество слагаемых 20, то сумма обоих сумм равна
2·S = (1+39)+(3+37)+(5+35)+ ... +(5+35)+(3+37)+(1+39) =
=40+40+40+...+40+40+40=40·20
или
S = 40·20:2= 800:2=400.
при 33, надо умножить на 7, т.к. 231:33=7