1. A = {x| x∈N, (x+1)² < 27}
т.к. x - натуральное число, то x≥1, то x+1≥2>0,
(x+1)²< 27
5²=25<27 < 36 = 6²
т.к. x - натуральное, то имеем
0<x+1≤5,
1≤x≤4;
A = {1; 2; 3;4},
|A| = 4;
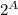= {∅, {1}, {2}, {3}, {4}, {1; 2}, {1; 3}, {1; 4}, {2; 3}, {2; 4}, {3; 4}, {1; 2; 3},
{1; 2; 4}, { 1; 3; 4}, {2; 3; 4}, {1; 2; 3; 4}}
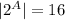
2. A = {0; 1; {2;3}}
B = {1; 2; 3}
C = {5; 6}
C-A = C\A = {5; 6},
A∩C = ∅,
B+C = BΔC = {1; 2; 3; 5; 6},
A - (B∪C) = A\(B∪C) = {0; 1; {2;3}}\{1; 2; 3; 5; 6} = {0; {2; 3}}.
3.
(A∩B)+(A∩C) = (A∩B)Δ(A∩C)
Пусть на дороге x пеньков, а мистер Фокс сидит на каждом y минут. Тогда мистер Форд сидит на каждом пеньке 2y минут.
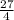часа = 405 минут потратит мистер Фокс на дорогу.
xy минут потратит мистер Фокс на отдых на пеньках.
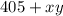минут всего потратит мистер Фокс.
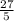часа = 324 минуты потратит мистер Форд на дорогу.
2xy минуты потратит мистер Форд на отдых на пеньках.
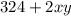минут всего потратит мистер Форд.
Вышли и пришли они одновременно, то есть
405+xy = 324+2xy
xy = 81
Так как x и y целые числа, то возможны следующие варианты:
1) x = 1, y = 81;
2) x = 3, y = 27;
3) x = 9, y = 9;
4) x = 27, y = 3
5) x = 81, y = 1.
Из предложенных вариантов подходят два: 1 и 3.
