Пошаговое объяснение:
f(x)= -x²+2x
для нахождения точек экстремумов используем первую производную
первая производная функции:
y' = 2-2x
2-2x=0⇒ х₁ = 1 точка экстремума
достаточное условие экстремума функции для определения минимум или максимум.
вторая производная:
y'' = -2
y''(1) = -2<0 - значит точка x = 1 точка максимума функции
y(1) = 1 - это максимум функции
монотонность у нас два интервала (-∞ ;1) и (1; +∞)
на каждом интервале берем точку и смотрим знак первой производной в этой точке
(-∞ ;1) y'(0) = 2 > 0 - функция возрастает
(1; +∞) y'(2) = -2 < 0 - функция убывает
б) 270
Пошаговое объяснение:
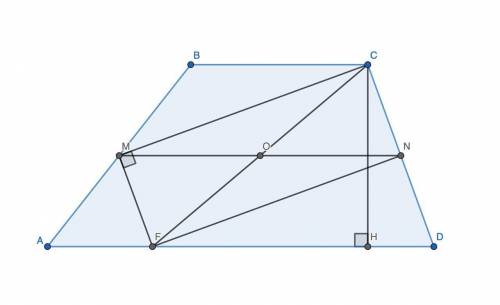
а) Пусть MN ∩ CF = O. MN — средняя линия ABCD ⇒ MN || AD. По теореме Фалеса MN || AD, CN = ND ⇒ CO = OF. В прямоугольном треугольнике CMF MO — медиана ⇒ MO = CF / 2 = MN / 2 ⇒ MO = ON. В четырёхугольнике CMFN CO = OF, MO = ON ⇒ CMFN — параллелограмм ⇒ MF || CN ⇒ MF || CD, что и требовалось доказать.
б) В прямоугольном треугольнике CMF tg ∠FCM = MF / MC = MF / 15 = 3 / 5 ⇒ MF = 9 ⇒ CD = 2CN = 2MF = 18. CF² = CM² + MF² = 9² + 15² = 306 ⇒ CF = √306 = 3√34 = MN. MF || CD, MF = CN = ND ⇒ MFDN — параллелограмм ⇒ FD = MN = 3√34.
CMFN — параллелограмм ⇒ ∠CMF = ∠FNC = 90° ⇒ FN ⊥ CD.
Пусть CH — высота трапеции, а значит, и треугольника FCD. Тогда 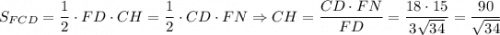
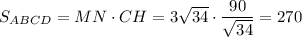
1) 3 2/5-1 1/3=3 6/15-1 5/15= 2 1/15=31/15
2) -6 1/5 / 31/15= -31/5 / 31/15 -31/5*15/31=-3
в) -3 2/3*1 1/2-1 2/3*1 1/2
1) -3 2/3* 1 1/2=-11/9*3/2=-11/6
2) 1 2/3* 1 1/2=6/3*3/2=3
3) -11/6-3=-1 5/6-3=-4 5/6