А1.
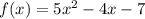
Найдём производную данной функции.

Найдём нули производной.
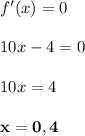
Определим знак производной на каждом промежутке.
- + 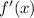
---------------------------------- ----------------------------------> x
----------------------------------> x
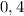
Функция возрастает там, где её производная положительна. А значит, она возрастает на промежутке 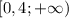 . Из перечня ответов полностью в этот промежуток входит только
. Из перечня ответов полностью в этот промежуток входит только  .
.
ответ: 3.
А2.
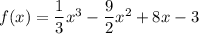
Найдём производную данной функции.
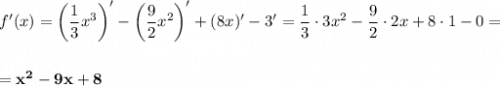
Найдём нули производной.
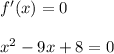
По теореме Виета:

Определим знак производной на каждом промежутке.
+ - + 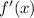
-------------------- -----------------------
----------------------- --------------------> x
--------------------> x

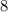
Функция убывает там, где её производная отрицательна. В нашем случае, на промежутке ![\bf{[1; 8]](/tpl/images/1729/3052/46b37.png) . Ему соответствует вариант номер 2.
. Ему соответствует вариант номер 2.
ответ: 2.
А3.
В точках минимума функция из убывания переходит в возрастание. На данном графике 4 такие точки (см. вложение).
ответ: 1.
А4.
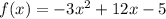
Найдём производную данной функции.
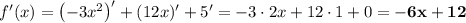
Найдём нули производной.
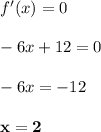
Точки максимума соответствуют точкам смены знака производной с плюса на минус. Проверим это, определив её знак на каждом промежутке:
+ - 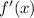
---------------------------------- ----------------------------------> x
----------------------------------> x
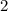
Полученные знаки соответствуют изложенному выше условию. Значит, 2 является точкой максимума функции.
ответ: 4.
А5.
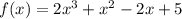
Найдём производную.
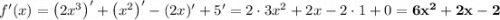
Найдём нули производной.

У производной нашлось 2 нуля. В то же время, производная равна нулю в точках экстремума графика функции. А значит, функция имеет две точки экстремума.
ответ: 1.
А6.
Точки максимума на графике производной соответствуют точкам смены знака производной с плюса на минус. На нашем графике это происходит в точке с абсциссой 3.
ответ: 2.
А7.
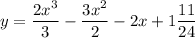
Найдём производную функции.
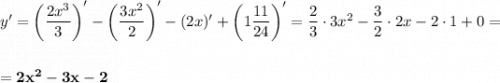
Найдём нули производной.
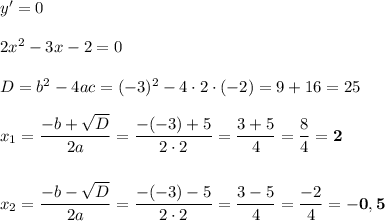
У производной нашлось 2 нуля. Найдём её знак на каждом промежутке.
+ - + 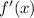
------------------ -------------------
------------------- -------------------> x
-------------------> x
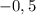
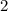
Точки минимума соответствуют точкам смены знака производной с минуса на плюс. Такой точке соответствует 2.
ответ: 4.
А8.
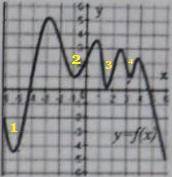
На заданном отрезке функция имеет одну точку максимума. Она соответствует значению функции, равному трём.
ответ: 2.
ответ:ответ:
а) 6 двухзначных чисел
б) 120 чисел
Пошаговое объяснение:
а) 3*2*1=6(ч)
это работает так потому что на 1 место можно поставить 3 цифры
на 2 место можно поставить 2 цифры
на 3 место можно поставить 1 цифру
и их можно перемножить потому что они друг от друга не зависят.
б)5*4*3*2*1=120(ч)
тоже самое.
на 1 место можно поставить 5 цифр
на 2 место можно поставить 4 цифры
на 3 место можно поставить 3 цифры
на 4 место можно поставить 2 цифры
на 5 место можно поставить 1 цифру
и их можно перемножить потому что они друг от друга не зависят.
Пошаговое объяснение: