Вступление
Пусть в прямоугольной трапеции ABCD, AB и CD основания, а ∠D прямой. Тогда AD меньшая боковая сторона (как расстояние между параллельными отрезками AB и CD), то есть AD=16см. По построению DC большое основание, поэтому по условию DC=31см. Острые углы при большом основании, ∠C=45° т.к. ∠D=90°.
H∈DC, BH⊥DC ⇒ BH=AD=16см.
В прямоугольном ΔBHC:
∠C=45°, ∠H=90° ⇒ ∠B=45°⇒ HC=BH=19см.
DH=DC-HC=31-16=15см.
В четырёхугольнике ABHD:
∠D=90°, ∠H=90° и ∠A=90°, ∠B=90° т.к. AB║DH, ведь H∈DC и AB║DC.
Получается ABHD - прямоугольник, поэтому AB=HD, HD=15см ⇒ AB=15см.
AB мень. осн. т.к. CD - большее.
Меньшее основание равно 15см.
Оценим максимальное значение, которое может принимать элемент множества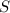 
. Предположим, что существуют хотя бы два элемента множества, больших 
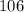. Пусть это числа 
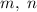. Положим 
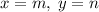, тогда 
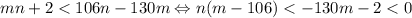, откуда 
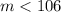. Противоречие. Значит, существует не более одного числа, большего
Теперь становится ясно, как строить множество. Пусть максимальное число равно 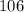. Тогда следующее по величине число меньше 
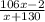, где 
— текущее число (сейчас рассматривается максимальное число; оценка следует из исходного уравнения). То есть второе по величине число не превосходит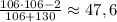 
. Берем 47. Далее: 
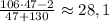. Берем 28. И так далее. Получим множество 
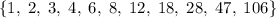, состоящее из 11 элементов. Это и есть наш ответ.
+
-4>-2
8+(-4)> 5+(-2)
4> 3