в числителе две одинаковые скобки в которых (у -х) .
Т.е. (у-х)²=(у-х)(у-х)
В знаменателе тоже есть почти такая же скобка, но с другим знаком, значит, если в числителе заменить (у-х)² на скобку (х-у)², то ничего не изменится. Верно? Возведите в квадрат пять. Получите 25, а минус пять возведите в квадрат. Опять двадцать пять), так и здесь, заменили квадрат на квадрат противоположного числа. и сократили на одну скобку . т.е. на (х-у)
осталось в числителе у²*(х-у) , в знаменателе после сокращения оставили у²(х+у). Видите, общий множитель у²? Вот на него и сокращайте. Итак, в ответе получили то, что справа записано в Вашем примере. Ясно ли?
777 литра
Пошаговое объяснение:
Пусть в 1-сосуде Х литр воды, а во 2-сосуде 0 литр воды.
1-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: 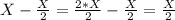
2-сосуд: 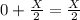
Объем воды в обоих сосудах в сумме дают Х литр!
2-переливание. Переливаем со 2-сосуда в 1-сосуд:
1-сосуд: 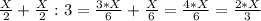
2-сосуд: 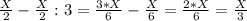
Объем воды в обоих сосудах в сумме дают Х литр!
3-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: 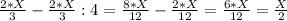
Так как, объем воды в обоих сосудах в сумме дают Х литр, то
2-сосуд: 
Теперь покажем, что в нечётных числах переливания всегда
1-сосуд: 
2-сосуд: 
Пусть n=2·k+1.
n-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: 
2-сосуд: 
(n+1)-переливание. Переливаем со 2-сосуда в 1-сосуд:
1-сосуд: 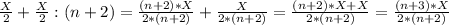
2-сосуд: 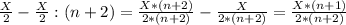
(n+2)-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: 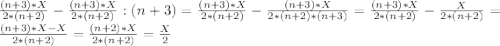
Так как, объем воды в обоих сосудах в сумме дают Х литр, то
2-сосуд: 
что требовалось показать.
Отсюда, 2019 - нечётное и X=1554 литра, тогда
1-сосуд: 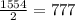
ывмям