Собственно, вот в этой задаче я уже решал, но почему-то пропали прикреплённые картинки. По этой причине повторюсь.
Если принять сторону основания за a, a ребро за b, то в зависимости от расчёта приходим к одной из формул (они приводимы друг к другу):
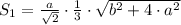
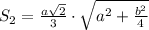
Сначала доказываете, что плоскость BMD перпендикулярна AC, далее - перпендикулярна A'C', A'C' пересекает BMD в точке P, ну и перпендикулярна всем прямым данной плоскости, проходящим через P => ND перпендикулярна A'C'.
Т.о. 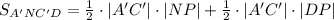
т.е. 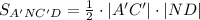
Найдём длины нужных нам в дальнейшем отрезков:
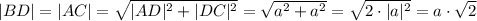
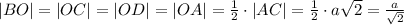
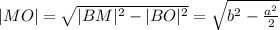
В треугольнике BMD DM и MO это медианы, пересекающиеся в точке P. Т.о. 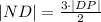
AC || A'C' из подобия треугольников AMC и A'MC' следует, что 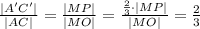
т.е. 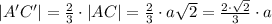
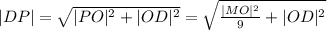
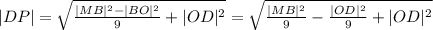
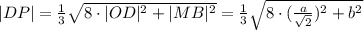
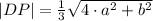
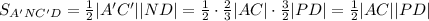
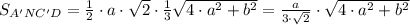
Теперь подставляем значения в формулу:
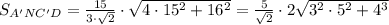
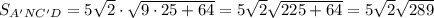
ответ: 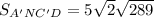
P.S.> Для примера - есть вариант, где a=6, b=12. В этом случае результат будет следующий:
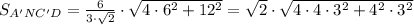
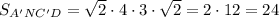
Это соответствует правильному ответу.
P.P.S.> Попробую прикрепить ещё снимки решения на бумаге (если получится) - там 2 варианта. Почему-то не всегда прикреплённые картинки сохраняются. По этому и вбил решение текстом.

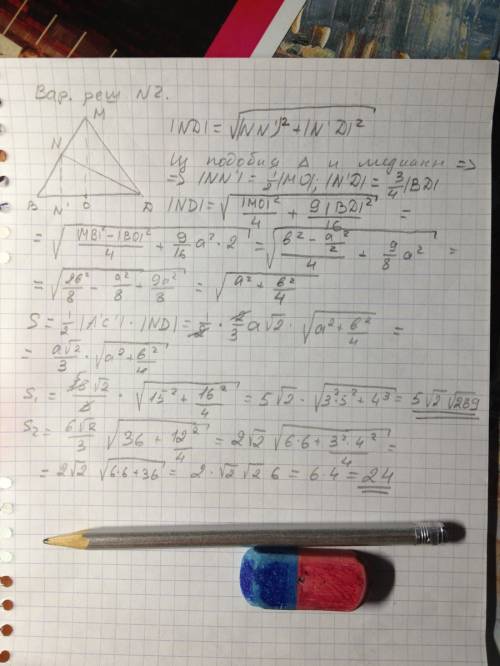
№1
самое маленькое натуральное число 1
Является ли число 0 натуральным? Нет, не является
Существует ли самое большое натуральное число? Нет, не существует
Как это можно доказать? Натуральные числа применяются при счете предметов, предметов может быть бесконечно много
Какое самое большое натуральное число ты можешь назвать? 999 миллиардов 999миллионов 999тысяч 999
Сколько <<значным>> является ето число? 12-значное
№2
Запиши самое маленькое и самое большое из натуральных чисел. 1 и не существует
Сколько всего существует пятизначных натуральных чисел? Как это число можно вычислить?
первое 10000, последнее 99999
(99999-10000)+1=90000
№3
Запиши все возможные числа с перестановки цифр в записи числа123. 123 132 213 231 312 321
Сколько таких чисел у тебя получилось? 6
Какое их этих чисел будет самым большим? 321
Каких чисел среди них больше: чётных или нечётных? нечетных
№4
Найди натуральное число, которое делится нацело на 2, 3 и 5. 2*3*5=30
№5
Найди натуральное число, которое при делении на 2, 3 и 5 даёт в остатке число 1. (2*3*5)+1=31
площа = ширина * довжина = 56*105 = 5880 м²