Сшили 8 платьев. на каждое платье пришили по 10 пуговиц. осталось 7 пуговиц. сколько пуговиц было?

👇

Увидеть ответ

Ответ:

Milenadaw

17.12.2020

1) 8×10 = 80 (п.) - потратили на 8 платьев
2) 80+7 = 87 (п.)
ответ. Всего было 87 пуговиц

4,4(47 оценок)

Ответ:

умная196

17.12.2020

Легкая задача.
Смотри.
У нас 8 платьев, если на каждое по 10.
1 платье = 10 пуговиц.
8 платьев = 80. ( 10 • 8 )
Осталось 7 пуговиц.
80 + 7 = 87.
Изначально было 87 пуговиц, 80 из которых пришили к 8 платьям поровну.
7 осталось.
ответ : 87.

4,6(69 оценок)

Открыть все ответы

Ответ:

VERONIKA81346

17.12.2020

Если переставить и 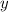местами, то получим ответ.

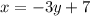$\begin{equation*}x =-3y+7\end{equation*}$ или, если выразить :

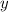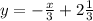$y = -\frac{x}{3} + 2\frac{1}{3}$ - ответ.

Пошаговое объяснение:

1. Найдем запись прямой L: 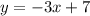y = -3x+7 в каноническом виде:

$y - 7 = -3x\\$ ,

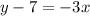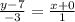$\frac{y-7}{-3} = \frac{x+0}{1}$ ,

L: 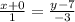$\frac{x+0}{1} = \frac{y-7}{-3}$ - канонический вид прямой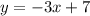 y = -3x+7

Каноническое уравнение прямой в общем виде 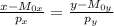$\frac{x - M_{0x}}{p_x} = \frac{y - M_{0y}}{p_y}$ .

Для нашей прямой точка 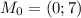M_0 = (0; 7) . (в числителе), вектор p = (1, -3) .

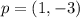Эти точка и вектор определяют саму прямую. Изменяя их, мы изменяем и прямую. Нам надо найти такие параметры 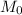M_0 и 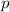, при которых получившаяся прямая - симметрична прямой L относительно y = x.

2. Произведем отображение относительно прямой F: y = x.

Определим угол поворота прямой F относительно начала координат:

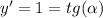$y' = 1 = tg(\alpha)$ ,

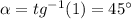$\alpha = tg^{-1}(1) = 45 \textdegree$ .

Процесс отображения протекает в 3 этапа:

Повернуть прямые так, чтобы F и OX сошлись;Отобразить относительно OX;Повернуть обратно

Делается это просто.

Представим оба наших параметра в виде матрицы

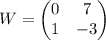
$\begin{equation*}W =\begin{pmatrix}0 & 7\\1 & -3\\\end{pmatrix}\end{equation*}$

Матрицы R, R' - матрицы поворота и обратного поворота. Матрица Т - матрица отражения относительно оси OX. Это "табличные" матрицы преобразований.

Параметры после преобразований рассчитываются умножением:

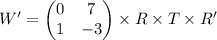
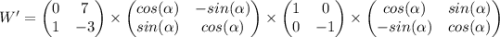
$\begin{equation*}W' =\begin{pmatrix}0 & 7\\1 & -3\\\end{pmatrix}\times R\times T\times R'$ $\begin{equation*}W' =\begin{pmatrix}0 & 7\\1 & -3\\\end{pmatrix}\times \begin{pmatrix}cos(\alpha) & -sin(\alpha)\\sin(\alpha) & cos(\alpha)\\\end{pmatrix}\times \begin{pmatrix}1 & 0\\0 & -1\\\end{pmatrix}\times \begin{pmatrix}cos(\alpha) & sin(\alpha)\\-sin(\alpha) & cos(\alpha)\\\end{pmatrix}\end{equation*}$

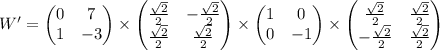
$\begin{equation*}W' =\begin{pmatrix}0 & 7\\1 & -3\\\end{pmatrix}\times \begin{pmatrix}\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\\\end{pmatrix}\times \begin{pmatrix}1 & 0\\0 & -1\\\end{pmatrix}\times \begin{pmatrix}\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\ -\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\\\end{pmatrix}\end{equation*}$

Осталось только провести расчеты:

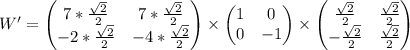
$\begin{equation*}W'=\begin{pmatrix} 7 * \frac{\sqrt{2}}{2} & 7 * \frac{\sqrt{2}}{2} \\-2 * \frac{\sqrt{2}}{2} & -4 * \frac{\sqrt{2}}{2} \\\end{pmatrix}\times \begin{pmatrix}1 & 0 \\0 & -1 \\\end{pmatrix}\times \begin{pmatrix} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\ -\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\\end{pmatrix}\end{equation*}\\$

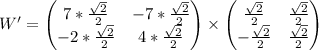
$\begin{equation*}W' =\begin{pmatrix} 7 * \frac{\sqrt{2}}{2} & -7 * \frac{\sqrt{2}}{2} \\-2 * \frac{\sqrt{2}}{2} & 4 * \frac{\sqrt{2}}{2} \\\end{pmatrix}\times \begin{pmatrix} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\ -\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\\end{pmatrix}\end{equation*}$

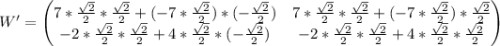
$\begin{equation*}W' =\begin{pmatrix} 7 * \frac{\sqrt{2}}{2} * \frac{\sqrt{2}}{2} + (-7 * \frac{\sqrt{2}}{2}) * (-\frac{\sqrt{2}}{2}) & 7 * \frac{\sqrt{2}}{2} * \frac{\sqrt{2}}{2} + (-7 * \frac{\sqrt{2}}{2}) * \frac{\sqrt{2}}{2} \\ -2 * \frac{\sqrt{2}}{2} * \frac{\sqrt{2}}{2} + 4 * \frac{\sqrt{2}}{2} * (-\frac{\sqrt{2}}{2}) & -2 * \frac{\sqrt{2}}{2} * \frac{\sqrt{2}}{2} + 4 * \frac{\sqrt{2}}{2} * \frac{\sqrt{2}}{2} \\\end{pmatrix} \end{equation*}$

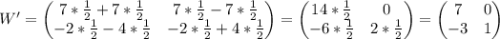
$\begin{equation*}W' =\begin{pmatrix} 7 * \frac{1}{2} + 7 * \frac{1}{2} & 7 * \frac{1}{2} - 7 *\frac{1}{2} \\ -2 * \frac{1}{2} - 4 * \frac{1}{2} & -2 * \frac{1}{2} + 4 * \frac{1}{2} \\\end{pmatrix}=\begin{pmatrix} 14 * \frac{1}{2} & 0 \\ -6 * \frac{1}{2} & 2 * \frac{1}{2} \\\end{pmatrix}=\begin{pmatrix} 7 & 0 \\ -3 & 1 \\\end{pmatrix}\end{equation*}$

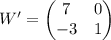
$W' = \begin{pmatrix} 7 & 0 \\ -3 & 1 \\\end{pmatrix}$

Мы получили новые параметры:

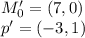
$M_0' = (7, 0)\\p' = (-3, 1)$

Подставим их в уравнение 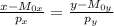$\frac{x - M_{0x}}{p_x} = \frac{y - M_{0y}}{p_y}$ :

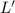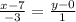: $\frac{x - 7}{-3} = \frac{y - 0}{1}$ или если выразить y, то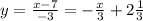 $y = \frac{x - 7}{-3} = -\frac{x}{3} + 2\frac{1}{3}$

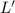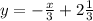
: $y = -\frac{x}{3} + 2\frac{1}{3}$

4,5(59 оценок)

Ответ:

МашаИвлеева789

17.12.2020

раскрыли скобки и привели подобные. просто это считают устно, поэтому может быть не ясно. Я распишу, и то, что является подобными, подчеркну. В числителе и знаменателе отдельно, потом соберу. Итак. от второго.

Числитель

2sinαcosβ-(sinα*cosβ-cosαsinβ)=

2sinα*cosβ-sinα*cosβ+cosαsinβ=sinα*cosβ+cosαsinβ=sin(α+β), привели подобные, и свернули по формуле синуса суммы двух углов.

Знаменатель

cosαcosβ+sinα*sinβ-2sinαsinβ=cosα*cosβ-sinα*sinβ=cos(α+β), привели подобные, и свернули по формуле косинуса суммы двух углов.

и последнее действие, аргументы одинаковые, значит, отношение равно тангенсу. sin(α+β)/cos(α+β)=tg(α+β)

4,6(74 оценок)

Это интересно:

Мир-работы

18.12.2022

Формула успешного бизнеса: как преуспеть в собственном бизнесе...

Здоровье