ДАНО: P= 16 см - периметр квадрата ABCD.
НАЙТИ: S(ABC) = ? - площадь треугольника.
РЕШЕНИЕ
Периметр квадрата по формуле:
Р = 4*а = 16 см
Находим сторону квадрата:
а = Р/4 = 16:4 = 4 см - сторона.
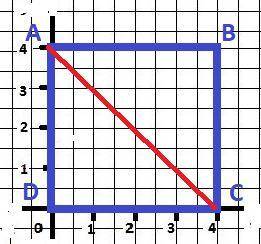
Начертили квадрат - рисунок в приложении.
1 см = 2 клетки в тетради. Обозначили вершины латинскими буквами. Провели диагональ квадрата АС .
ΔАВС = ΔADC - равные по двум сторонам и углу между ними, равнобедренные.
Площадь треугольника по формуле:
S(ABC) = 1/2*a*b = 1/2*a² = 4*4/2 = 8 см² - площадь треугольника - ОТВЕТ
ответ:
с контрольной на завтра, нет времени пишу даже данный текст был скопирован с документа txt
1.из уравнений биквадратным с:
а)x⁴ - x + 1 = 0
б)x⁴ - x³ - 1 =0
в)x⁴ - 4x² + 6 = 0
г)другое
2.якщо в рівнянні x⁴-10x²+9=0 зробити заміну x²=t то дістанемо рівняння
а)t⁴ - 10t +9 = 0
б)t² - 10t = 0
в)t² - 10t + 9 = 0
г)другое
3.разложите на множители выражение
8x² -6x -2
4.сократите дробь
x²- 6x +5
x² -25
5.решите уравнение
x⁴ - 12x² + 27 = 0
пошаговое объяснение:
способ.
все рациональные (в данном случае целые) решения должны являться делителями свободного члена (четвёрки) .
т, е. все целые решения могут быть равны ±1, ±2, ±4.
подбором убеждаемся, что x₁=2 и x₂=−2 являются корнями уравнения.
разделив (столбиком) исходный многочлен на (x−2)(x+2) = (x²−4), получим:
x⁴ − x³ − 3x² + 4x − 4 = (x²−4)(x²−x+1) = 0
решая уравнение x²−x+1 = 0, получаем, что других действительных корней уравнение не имеет (дискриминант d=1−4=−3< 0).
но есть ещё два комплексно-сопряжённых корня
x₃,₄ = (1±i√3)/2.
ii способ.
разложим многочлен на множители, сгруппировав слагаемые:
x⁴ − x³ − 3x² + 4x − 4 = x²(x²−4) + (x²−4) − x(x²−4) = (x²−x+1)(x²−4).
отсюда получаем те же корни, чо и в i способе.
ответ: два действительных корня x₁,₂ = ±2
и два комплексно-сопряжённых корня
x₃,₄ = (1±i√3)/2.