![\left[\begin{array}{cccc}2&1&4&8\\-2&-1&3&-3\\4&-4&0&5\\6&2&2&-1\end{array}\right]](/tpl/images/1382/4549/c8f1f.png)
Вычитаем из 2, 3 и 4 строки первую, умноженную на -1, 2 и 3 соответственно:
![\left[\begin{array}{cccc}2&1&4&8\\0&0&7&-5\\0&-6&-8&-11\\0&-1&-10&-25\end{array}\right]](/tpl/images/1382/4549/867c4.png)
Умножаем первый столбец на 1/2:
![\left[\begin{array}{cccc}1&1&4&8\\0&0&7&-5\\0&-6&-8&-11\\0&-1&-10&-25\end{array}\right]](/tpl/images/1382/4549/dbaab.png)
Вычитаем из 2, 3 и 4 столбца первый, умноженный на 1, 4 и 8 соответственно:
![\left[\begin{array}{cccc}1&0&0&0\\0&0&7&-5\\0&-6&-8&-11\\0&-1&-10&-25\end{array}\right]](/tpl/images/1382/4549/64ecb.png)
Поменяем местами вторую и четвертую строку и умножим вторую строку на -1:
![\left[\begin{array}{cccc}1&0&0&0\\0&1&10&25\\0&-6&-8&-11\\0&0&7&-5\end{array}\right]](/tpl/images/1382/4549/fae39.png)
Прибавим к третьей строке вторую, умноженную на 6:
![\left[\begin{array}{cccc}1&0&0&0\\0&1&10&25\\0&0&52&139\\0&0&7&-5\end{array}\right]](/tpl/images/1382/4549/bbe91.png)
Вычтем из 3 и 4 столбца второй, умноженный на 10 и 25 соответственно:
![\left[\begin{array}{cccc}1&0&0&0\\0&1&0&0\\0&0&52&139\\0&0&7&-5\end{array}\right]](/tpl/images/1382/4549/13c81.png)
Умножим третью строку на 1/52:
![\left[\begin{array}{cccc}1&0&0&0\\0&1&0&0\\0&0&1&\frac{139}{52} \\0&0&7&-5\end{array}\right]](/tpl/images/1382/4549/34646.png)
Вычтем из четвертой строки третью, умноженную на 7:
![\left[\begin{array}{cccc}1&0&0&0\\0&1&0&0\\0&0&1&\frac{139}{52} \\0&0&0&-5-\frac{973}{52} \end{array}\right]](/tpl/images/1382/4549/d55fc.png)
![\left[\begin{array}{cccc}1&0&0&0\\0&1&0&0\\0&0&1&\frac{139}{52} \\0&0&0&-\frac{1233}{52} \end{array}\right]](/tpl/images/1382/4549/3fe86.png)
Вычтем из четвертого столбца третий, умноженный на 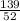 :
:
![\left[\begin{array}{cccc}1&0&0&0\\0&1&0&0\\0&0&1&0 \\0&0&0&-\frac{1233}{52} \end{array}\right]](/tpl/images/1382/4549/c0681.png)
Умножим четвертую строку на 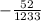 :
:
![\left[\begin{array}{cccc}1&0&0&0\\0&1&0&0\\0&0&1&0 \\0&0&0&1 \end{array}\right]](/tpl/images/1382/4549/96346.png)
Ранг матрицы равен четырем, привели к каноничному виду при элементарных преобразований.
(12650+2530)* 1/6=2530 дубів на обох ділянках