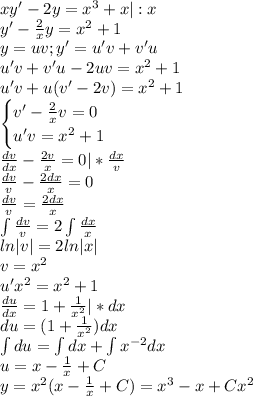

Все просто)
Обозначим расстояние от А до Б в х км. Мотоциклист за первые два час проехал 80 км, поэтому его скорость была равна V = 80/2 = 40 км/ч. С такой скоростью он преодолел бы все расстояние за x/40 часов, опоздав на 15 минут, то есть точное время составило бы x/40 - 15/60 часов. Оставшийся путь (х - 80) км он проехал со скоростью V = 40 + 10 = 50 км/ч
. Поэтому, время, за которое он проехал полное расстояние от А до В составило: 2 + (х - 80)/50 часов и это на 36 мин. раньше, чем ожидалось. Поэтому запланированное время было: 2 + (х -80)/ 50 + 36/60 Когда мы приравняем выражения для ожидаемого времени, мы получим уравнение:
x/40 – 15/60 = 2 + (x -80)/50 + 36/60 <=> (x - 10)/40 = (100 + x - 80 + 30)/50 <=> (x - 10)/4 = (x +50)/5 <=> 5x - 50 = 4x + 200 <=> x = 250
Итак, искомое расстояние равно 250 км. Время возможно найти, заменив x на 250 в первом выражении, например:
x/40 – 15/60 = 250/40 – 1/4 = 25/4 – 1/4 = 24/4 = 6 часов.
Пошаговое объяснение:
Уравнение неоднородное 1 порядка.
Замена y = u*v, y' = u'*v + u*v'
x*u'*v + x*u*v' - 2u*v = x^3 + x
x*u'*v + u*(x*v' - 2v) = x^3 + x
Скобку приравниваем к 0
x*v' - 2v = 0
x*dv/dx = 2v
dv/v = 2dx/x
ln v = 2ln x = ln(x^2)
v = x^2
Подставляем в уравнение
x*u'*x^2 + u*0 = x^3 + x
u'*x^3 = x^3 + x
u' = 1 + 1/x^2
Решаем интегрированием
u = x - 1/x + C
Обратная замена
y = u*v = (x - 1/x + C)*x^2 = x^3 + Cx^2 - x
б) y'' - 12y' + 36y = 14e^(6x)
Неоднородное уравнение 2 порядка
y = y0 + y* (решение однородного + частное решение неоднородного)
Однородное
y'' - 12y' + 36y = 0
Характеристическое уравнение
k^2 - 12k + 36 = 0
(k - 6)^2 = 0
k1 = k2 = 6
y0 = (C1 + C2*x)*e^(6x)
Находим частное решение неоднородного уравнения
Степень е равна 6x, 6 - кратный корень характеристического уравнения
y* = Ax^2*e^(6x) (A - это неизвестный коэффициент)
y*' = A(2x*e^(6x) + x^2*6e^(6x)) = A(2x + 6x^2)*e^(6x)
y*'' = A[(2 + 12x)*e^(6x) + (2x + 6x^2)*6e^(6x)] =
= A(2 + 12x + 12x + 36x^2)*e^(6x)
Подставляем в уравнение
A(2+24x+36x^2)*e^(6x) - 12A(2x+6x^2)*e^(6x) + 36Ax^2*e^(6x) = 14e^(6x)
Сокращаем e^(6x)
A(2 + 24x + 36x^2) - 12A(2x + 6x^2) + 36Ax^2 = 14
Раскрываем скобки
2A + 24Ax + 36Ax^2 - 24Ax - 72Ax^2 + 36Ax^2 = 14
2A = 14
A = 7
y* = 7x^2*e^(6x)
Окончательный ответ
y = y0 + y* = (C1 + C2*x)*e^(6x) + 7x^2*e^(6x)