1. Пусть было х трехместных и у пятиместных лодок.
x+y = 7
В трехместные лодки поместилось 3x чел, а в пятиместные 5y чел. Всего в лодках был 31 турист.
3x+5y = 31
Составим и решим систему уравнений:
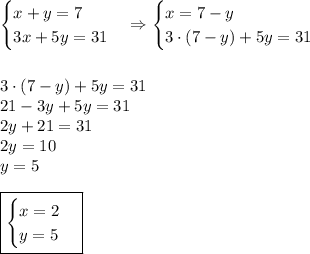 .
.
ответ: было 2 пятиместных и 5 трёхместных лодок.
2. Собственная скорость катера x км/ч, скорость течения реки y км/ч.
x+y км/ч скорость катера по течению
x-y км/ч скорость катера против течения
По течению 84 км проплыл за 3 часа:
(x+y)·3 = 84
Против течения 84 км проплыл за 3,5 часа:
(x-y)·3.5 = 84
Составим и решим систему уравнений:
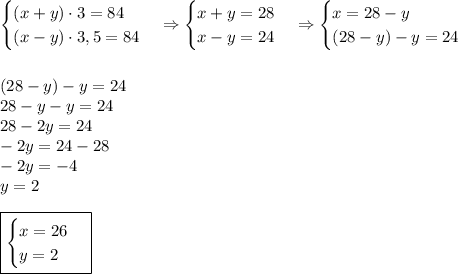
ответ: собственная скорость катера 26 км/ч, скорость течения реки 2км/ч.
1. Пусть было х трехместных и у пятиместных лодок.
x+y = 7
В трехместные лодки поместилось 3x чел, а в пятиместные 5y чел. Всего в лодках был 31 турист.
3x+5y = 31
Составим и решим систему уравнений:
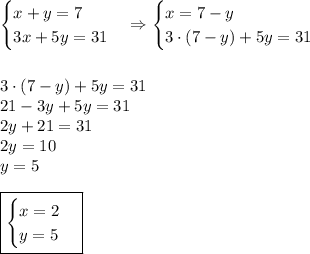 .
.
ответ: было 2 пятиместных и 5 трёхместных лодок.
2. Собственная скорость катера x км/ч, скорость течения реки y км/ч.
x+y км/ч скорость катера по течению
x-y км/ч скорость катера против течения
По течению 84 км проплыл за 3 часа:
(x+y)·3 = 84
Против течения 84 км проплыл за 3,5 часа:
(x-y)·3.5 = 84
Составим и решим систему уравнений:
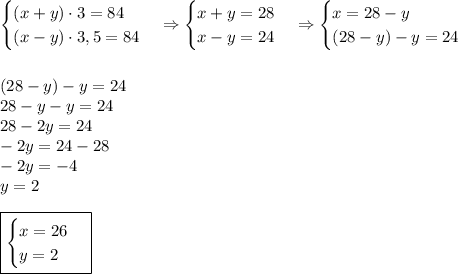
ответ: собственная скорость катера 26 км/ч, скорость течения реки 2км/ч.
1 - 0,3 = 0,7 часть составляет остаток после 1-го дня
2) 40% = 40/100= 0,4
0,4 * 0,7 = 0,28 часть прочитана во 2-й день
3) 1 - (0,3 + 0,28) = 1 - 0,58 = 0,42 часть составляет 105 страниц
4) 105 : 0,42 = 250 (стр.) в книге
Пусть в книге х страниц.
Первый день 0,3х
Второй день 0,4(х -0,3х)
Третий день 105 страниц
Уравнение.
х - 0,3х - 0,4(х-0,3х) = 105
х - 0,3х - 0,4х +0,12х = 105
х* (1 - 0,3 - 0,4 + 0,12) = 105
0,42х = 105
х= 105/0,42 = 10500/42
х=250 (стр.) в книге
ответ: 250 страниц в книге.