Дана функция y = 2x/(x² + 1.
Функция нечетная.
Условия для точек разрыва : x² + 1 = 0, x² = -1.
Точки разрыва : нет.
Корни функции (точки пересечения с осью абсцисс x) : x = 0.
Вычисление y′ : y′=2⋅1(x²+1)−x(2x)(x²+1)2=2⋅1−x²(x²+1)2=−2(x−1)(x+1)(x2+1)2
Первая производная : y′=−2(x−1)(x+1)/(x²+1)²
Условия для стационарных точек : −2(x−1)(x+1)=0
Стационарные точки : х1=−1, х2=1
Вторая производная : y′′=4x(x²−3)/(x²+1)³
Условия для критических точек : 4x(x²−3)=0
Критические точки : х1=−√3, х2=√3, х3=0
Асимптота на обоих ±∞ линия y=0.
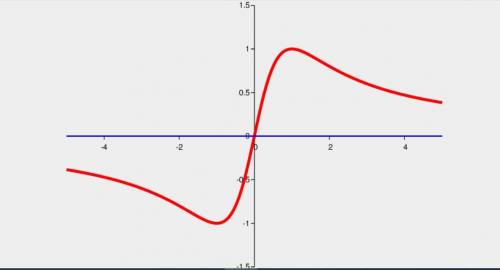
ответ
Пусть х км/ч - скорость пешехода, тогда (х-2) км/ч - скорость туриста
Пусть у ч - время туриста, тогда (у - 0,5) ч - время пешехода.
По условию ясно, что пешеход км, а турист соответственно км. Составим уравнения:
12/(х-2) - это время туриста, 15/х - это время пешехода.
Составим систему уравнений:
у = 12/(х-2)
у-0,5 = 15/х
Подставим первое во второе, получим:
12/(х-2) - 0,5 = 15/х
Перенесем:
12/(х-2) - 15/х = 0,5
под общий знаменатель:
(12х - 15х + 30) / х (х-2) = 0,5
30 - 3х = 0,5х (2) - х
х (2) - это х в квадрате
-3х - 0,5х (2) + х + 30 = 0
-0,5х (2) - 2х + 30 = 0
0,5х (2) + 2х - 30 = 0
х (2) + 4х - 60 = 0
Д = 16 + 4*60 = 256
корень из Д = 16
х первый = (-4 + 16) / 2 = 6 км/ч
х второй = (-4-16)/2 = -10 - не подходит, т. к. отрицательный
Значит скорость пешехода х = 6 км/ч
скорость туриста = 6-2 = 4 км/ч
Пошаговое объяснение: