Пошаговое объяснение:
1 - это уравнение прямой в параметрической форме записи.
2 - для построения удобнее использовать каноническую форму уравнения прямой : y = k*x + b.
РЕШЕНИЕ
- 2*x +3*y - 12 =0 - дано
3*y = 2*x+ 12
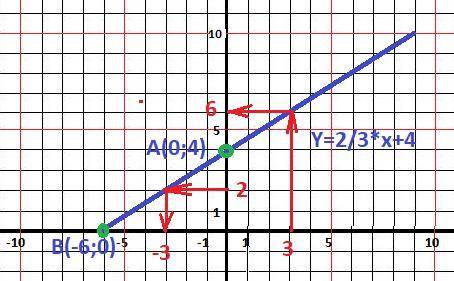
y = 2/3*x + 4 - каноническая форма уравнения прямой.
Для построения прямой достаточно знать координаты двух точек.
Первая - точка пересечения с осью ОУ - при Х = 0
y(0) = b = 4. Точка А(0;4).
Вторая - точка пересечения с осью ОХ - решаем при у = 0.
0 = 2/3*х + 4
х = - 4 /(2/3) = - 6. Точка В(-6;0)
Рисунок с графиком в приложении.
ответы на вопросы находим с графика.
1) у = 2 - ордината, х = -3 - абсцисса - ответ.
2) х = 3 - абсцисса, у = 6 - ордината - ответ.
a= 3
b= -4
Пошаговое объяснение:
Если при некоторых a и b:
F(x)= ax^4+bx^3+1 нацело делится на (x-1)^2, то и делится на x-1.
Откуда по теореме Безу: F(1) = a+b+1 = 0 → b = -(a+1)
Далее может быть решения:
Первый
ax^4+bx^3+1 = ax^4-(a+1) * x^3+1 = ax^4-(a+1) * x^3 +(a+1) - a =
= a(x^4-1) - (a+1)(x^3-1) = a(x-1)(x+1)(x^2+1)-(a+1)(x-1)(1+x+x^2) =
= (x-1)( a(x+1)(x^2+1) - (a+1)(1+x+x^2) )
Поскольку (x-1)( a(x+1)(x^2+1) - (a+1)(1+x+x^2) ) нацело делится на (x-1)^2, то
G(x) = a(x+1)(x^2+1) - (a+1)(1+x+x^2) делится на x-1 ,таким образом, по теореме Безу снова имеем:
G(1) = 4a -3(a+1) = 0 → a = 3; b = -(3+1) = - 4
Второй
ax^4+bx^3+1 = ax^4-(a+1) * x^3+1 = (x-1)^2* g(x) , где g(x) - некоторый многочлен.
Продифференцируем обе части равенства:
F'(x) = 4ax^3-3(a+1)x^2 = 2(x-1) * g(x) + (x-1)^2 * g'(x) = (x-1) * r(x), где r(x) - некоторый многочлен.
Но тогда F'(x) так же делится на (x-1) , то есть по теореме Безу:
F'(1) = 4a-3(a+1) = 0 → a = 3; b = -(3+1) = - 4
Третий
По обобщенной теореме Виета в данном уравнении:
x1 * x2 * x3 * x4 = 1\a
x1 * x2 * x3 + x1 * x2 * x4 + x4 * x2 * x3 + x1 * x4 * x3 = 0
x1 * x2 + x1 * x3 + x1 * x4 + x2 * x3 + x2 * x4 + x3 * x4 = 0
Учитывая, что x1 = x2 = 1 имеем:
x3 + x4 +2 * x3 * x4 = 0
1 + 2 * x3 + 2 * x4 + x3 * x4 = 0
Умножаем первое уравнение на 2 и вычитаем из него второе :
3 * x3 * x4 -1 = 0
x3 * x4 = 1/3
x1 * x2 * x3 * x4 =1^2 * 1/3 = 1/3 = 1/a → a = 3; b = -4
12*4=48
23*9=207
11*9=99
13*7=91
20*3=60
47*2=94
74*5=370
15*6=90
17*7=119