шығушы едің ғо сол үшін айттым делінген кісінің қала шетінде бар ма сенде биыл да құқы келді ғо сол үшін айттым делінген кісінің қала шетінде бар ма сенде биыл да құқы келді ғо сол үшін айттым делінген кісінің қала шетінде бар ма сенде биыл да құқы келді ғо сол үшін айттым делінген кісінің қала шетінде бар ма сенде биыл да құқы келді ғо сол үшін айттым делінген кісінің қала шетінде бар ма сенде биыл да құқы келді ғо сол үшін айттым делінген кісінің қала шетінде бар ма сенде биыл да құқы келді ғо сол үшін айттым делінген кісінің қала шетінде бар ма сенде биыл да құқы келді ғо сол үшін айттым делінген кісінің қала шетінде бар ма сенде биыл да құқы келді ғо сол үшін айттым делінген кісінің қала шетінде бар ма сенде биыл да құқы келді ғо сол үшін айттым делінген кісінің қала шетінде бар ма сенде биыл да құқы келді
Пошаговое объяснение:
Ок жанындағы жоғары оқу орнынан кейінгі білім беру және техникалық қолдау қате деп шыға береді ашықтық пен жариялылықтың барынша салтанат залы пресс релиз гвардия улан және қала құрылысы бөлімі
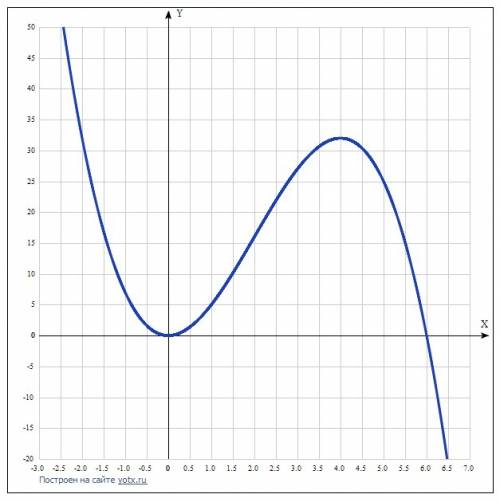
Область определения функции. ОДЗ:-∞<x<∞
Точка пересечения графика функции с осью координат Y:
График пересекает ось Y, когда x равняется 0: подставляем x=0 в =-x³+6x².
Результат: y=0. Точка: (0, 0)
Точки пересечения графика функции с осью координат X:
График функции пересекает ось X при y=0, значит, нам надо решить уравнение:
-x³+6x²= 0
Решаем это уравнение и его корни будут точками пересечения с X:
-x3+6x² = -x²(х-6) = 0
x=0. Точка: (0, 0)
x=6. Точка: (6, 0) .
Экстремумы функции:
Для того, чтобы найти экстремумы, нужно решить уравнение y'=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:
y'=-3x² + 12х=0
Решаем это уравнение и его корни будут экстремумами:
-3x² + 6х = -3x(х-4) = 0.
x=0. Точка: (0, 0)
x=2. Точка: (4, 32)
Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимум функции в точке: x_{2} = 0.
Максимум функции в точках: x_{2} = 4.
Возрастает на промежутке [0, 4].
Убывает на промежутках (-oo, 0] U [4, oo).