Вычислите:
1) sin 105° * sin 75°; 2) 4sin 37,5° * sin 7,5°; 3) 8sin 22,5° * cos 7,5°
1 ) sin 105° * sin 75° = (1/2)* (cos(105° -75°) - cos(105°+75°) )=
(1/2)* (cos30°-cos180°) =(1/2)* ( (√3)/ 2 - (-1) ) = (1/2)*((√3) / 2+ 1 ) = (√3+2)/4
- - - - - - -
2 ) 4sin 37,5° * sin 7,5° =2*(cos(37,5° - 7,5°) - cos(37,5° +7,5°) ) =
2*(cos30° - cos45°) =2*( (√3)/2 -(√2) /2) = √3 - √2 .
- - - - - - -
3 ) 8sin 22,5° * cos 7,5° = 4*( sin(22,5°+7,5°) +sin(22,5°-7,5°) ) =
4*( sin30° + sin15° ) = 4*( 1/2 + sin(60 - 45°) ) =
4*( 1/2 + sin60°*cos45°- cos60°*sin45° ) = || cos45°=sin45 =√2 / 2 ||
= 4*( 1/2 + √2 (√3 - 1) / 4 ) = 2 + √6 - √2 .
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
P.S. sin15° =sin(45° -30°) = sin45°*cos30° - cos45°* sin30° =
(√2 / 2)*(√3 / 2 -1 / 2) = (√6 - √2) / 4 .
sin15° =√( (1 -cos30°) / 2 ) =√( (1 -√3 /2) / 2 ) =√( (2-√3 ) / 4 ) =
√( (4-2√3 ) / 8 ) =√( (3-2√3+1) / 8 ) =√( (√3 - 1 )² / 8 ) = (√3 - 1) /2√2 =
√2(√3 - 1) /4 = (√6 - √2) / 4 .
В решении.
Пошаговое объяснение:
Вопросы теме " Функции".
Для каждой из трех функций ( прямо пропорциональная зависимость, линейная, обратно пропорциональная зависимость, запишите:
1. формулу, задающую эту зависимость;
2. что является графиком данной функции;
3. нарисуйте график каждой функции;
4. как определить, проходит ли график через данную точку.
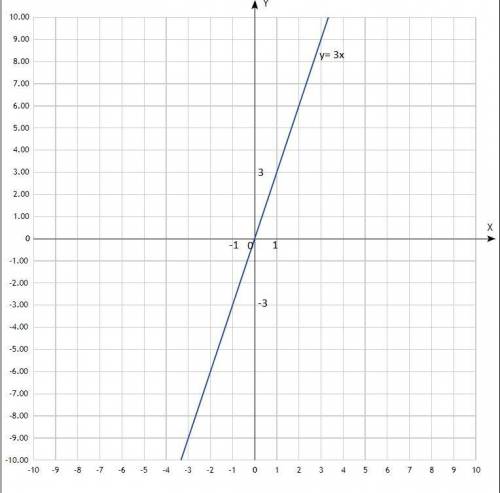
1) Прямо пропорциональная зависимость: у = kх; график - прямая, проходящая через начало координат.
Построить график. График линейной функции, прямая линия. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
у = 3х;
Таблица:
х -1 0 1
у -3 0 3
По вычисленным точкам построить прямую.
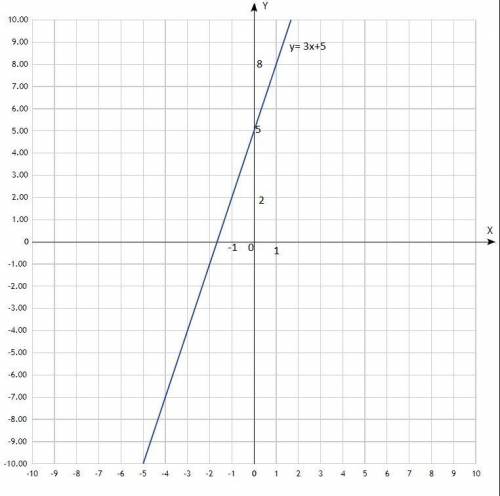
2) Линейная функция: у = kx + b; график - прямая линия.
Построить график. График линейной функции, прямая линия. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
у = 3х + 5;
Таблица:
х -1 0 1
у 2 5 8
По вычисленным точкам построить прямую.
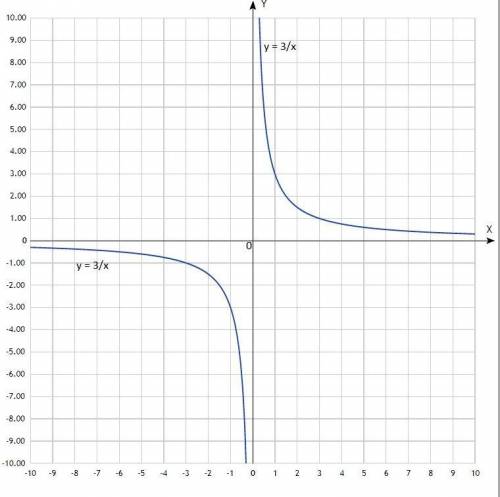
3) Обратно пропорциональная зависимость: у = k/x; график - гипербола, состоящая из двух ветвей.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = 3/х;
Таблица:
х -10 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 10
у -0,3 -0,5 -0,6 -0,75 -1 -1,5 -3 - 3 1,5 1 0,75 0,6 0,5 0,3
По вычисленным точкам построить гиперболу.
4) Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение. Если левая часть равна правой, то принадлежит, и наоборот.