Берешь любую карту и линейкой меряешь расстояние между Москвой и Киевом в сантиметрах и потом умножаешь на масштаб (большее число в отношении записывается обычно в правом нижнем углу карты например 1:10 000 000). Получаешь расстояние выраженное в сантисметрах и потом его переводишь в километры путем деления получившегося числа на число сантиметров в одном километре (100 000).
Должно получиться около 760 км (если карта будет с масштабом который я указал, то на карте это расстояние будет измерено линейкой как 7 см и 6 мм).
Здесь за одно и то-же время было два движения:
1. Фляга со скоростью течения реки (обозначим X) проплыла от первого моста (момент потери) до воторого (пловец ее догнал) 1км. Т.о. можно вычислить время за которое это проихошло как: 1/X ч.
2. Пловец вначале 10 минут (10/60=1/6) или 1/6 часа плыл против течения со скоростью Y-X, где Y - собственная скорость пловца в стоячей воде). За это время он проплыл расстояние (1/6)*(Y-X). Потом он повернул обратно и за оставшееся время проплыл путь длиной 1+(1/6)*(Y-X) со скоростью Y+X (т.к. он плыл уже по течению). Это оставшееся время можно найти как (1+(1/6)*(Y-X))/(Y+X).
Все это можно совместить следущим образом:
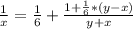
Осталось найти из этого X:
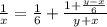
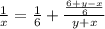
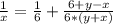
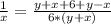
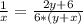
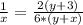
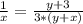
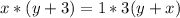
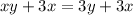
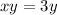
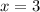
ОТВЕТ 3 км/ч
Нужно максимизировать f(x) = (75 - x) * √x, где x лежит в отрезке [0, 75]
Не люблю возиться с корнями, буду рассматривать функцию g(x) = (f(x))², очевидно, у неё максимум там же, где и у f(x).
g(x) = (75 - x)² x = x³ - 150x² + 75² x
g'(x) = 3x² - 300x + 75² = 0
x² - 100x + 25 * 75 = 0
Повезло: по теореме Виета сразу угадались корни x = 25, x = 75.
Знаки производной:
[0] -- (+) -- [25] -- (-) -- [75]
В точке x = 25 производная меняет знак с + на -, это точка локального максимума. Понятно, что там же достигается и максимум на отрезке [0, 75].
ответ: надо разложить на 50 и 25.