Пусть числитель дроби равен х, тогда ее знаменатель равен (х + 1) и дробь будет равна x/(x + 1).
Если числитель возвести в квадрат, то он будет равен x^2, а знаменатель увеличить на 4, то он будет равен (x + 1) + 4 = x + 5, и дробь будет такой: x^2/(x + 5). Если получившуюся дробь умножить на дробь, обратную исходной, то получится x^2/(x + 5) * (x + 1)/x или 3/2. Составим уравнение и решим его.
x^2/(x + 5) * (x + 1)/x = 3/2;
x(x + 1)/(x + 5) = 3/2 – применим основное свойство пропорции: Произведение крайних членов пропорции равно произведению средних членов пропорции;
2x(x + 1) = 3(x + 5);
2x^2 + 2x = 3x + 15;
2x^2 + 2x – 3x – 15 = 0;
2x^2 – x – 15 = 0;
D = b^2 – 4ac;
D = (- 1)^2 – 4 * 2 * (- 15) = 1 + 120 = 121; √D = 11;
x = (- b ± √D)/(2a);
x1 = (1 + 11)/(2 * 2) = 12/4 = 3;
x2 = (1 – 11)/4 = - 10/4 = - 2,5.
х1 и х2 – это числители, найдем знаменатели.
x1 + 1 = 3 + 1 = 4;
x2 + 1 = - 2,5 + 1 = - 1,5.
Если числитель – 2,5, а знаменатель – 1,5 – то дробь будет сократимой, что противоречит условию. Значит, исходная дробь равна 3/4. Произведение числителя и знаменателя равно 3 * 4 = 12.
ответ. 12.
а) При значении а = -6 уравнение имеет корень равный 2.
При значении а = 16 уравнение имеет корень равный -3/4.
При значении а = 60 уравнение имеет корень равный -0,2.
b) При значении а = 0 уравнение не имеет корней.
c) При а > 0 уравнение будет иметь отрицательный корень.
Пошаговое объяснение:
Требуется найти, при каких значениях а уравнение
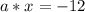 :
:
а)
1. Имеет корень, равный 2.
Подставим вместо х его значение 2 и решим уравнение относительно а:
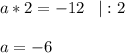
⇒ При значении а = -6 уравнение имеет корень равный 2.
2. Имеет корень, равный 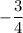 .
.
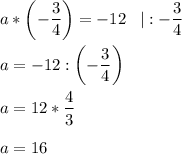
⇒ При значении а = 16 уравнение имеет корень равный 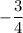 .
.
3. Имеет корень, равный -0,2.
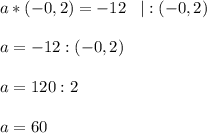
⇒ При значении а = 60 уравнение имеет корень равный -0,2.
b) Не имеет корней.
Уравнение не имеет решения, если при любом значении х, мы не получим верного равенства.Это возможно только тогда, когда а = 0.
Проверим:
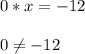
⇒ При значении а = 0 уравнение не имеет корней.
с) Имеет отрицательный корень.
Правая часть у нас отрицательная.
При нахождении корня, мы делим правую часть на а. Чтобы корень был отрицательным, то а должно быть положительным.
При делении чисел с разными знаками, частное - отрицательно.⇒ а > 0
⇒ При а > 0 уравнение имеет отрицательный корень.
-11/18+(20/9)*2/10=-11/18+4/9=-11/18+8/18=-3/18=-1/6
Далее:
6*0,2/(6*6*6)=0,2/(6*6)=0,1/18=1/180