1) 500 км
2) 4 часов
3) 100 км/ч
4) 25 км/ч
Пошаговое объяснение:
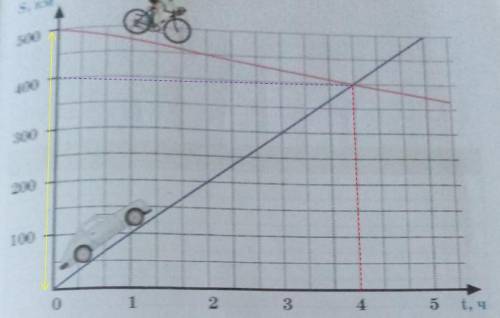
На рисунке (см. в приложении) каждые 2 клетки равны 100 км, а 3 клетки равны 1 часу.
1) Между автомобилем и велосипедистом в начале пути было 500 км (расстояние указывает жёлтая линия);
2) Они встретились через t=4 часов (указывает красная линия);
Они встретились в отметке 400 км (указывает лиловая линия). Тогда автомобиль проехал S₁=400 км, а велосипедист S₂=500-400=100 км.
Расстояние S, пройдённое объектом, связана со скоростью υ и временем t по формуле:
S = υ · t.
Отсюда находим скорость υ через расстоянием S и временем t:
υ = S / t.
Тогда:
3) Скорость автомобиля равна:
υ₁ = S₁ / t = 400 км/ 4 ч = 100 км/ч;
4) Скорость велосипедиста равна:
υ₂ = S₂ / t = 100 км/ 4 ч = 25 км/ч.
ВС₁ - диагональ грани куба, равная а√2.
Площадь сечения АВС₁Д₁ = 81√2 = а*а√2 = а²√2.
Отсюда а =√81 = 9.
а) Диагональ куба равна а√3 = 9√3.
б) площадь сечения куба плоскостью ACD' - это равносторонний треугольник со сторонами, равными диагоналям граней у вершины Д.
Площадь равностороннего треугольника равна (а√2)²√3)/4 = 81√3/2