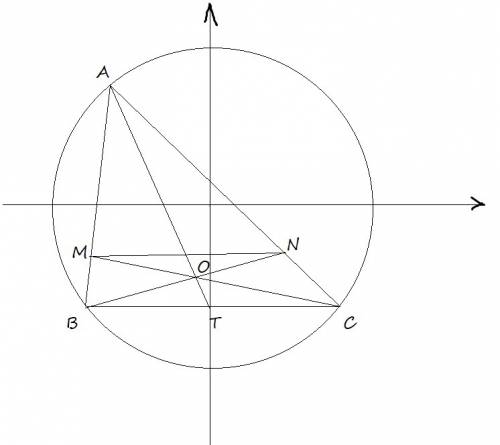
Поскольку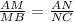 
, то треугольники MAN и BAC подобны. Значит MN параллелен BC ⇔ BMNC - трапеция. При этом BN и MC - диагонали. В трапеции отрезок, соединяющий середины оснований, продолжения боковых сторон и точка пересечения диагоналей лежат на одной прямой. Следовательно, AT - медиана треугольника ABC. Заметим, что отношение "расстояний" пройденных точками A и O равно искомому отношению диаметров окружностей, что равно отношению радиусов. Точка T зафиксирована. Спроецируем путь пройденный точкой O на вертикальную ось. Получим длину диаметра окружности. Данный диаметр пропорционален длине отрезка OT. Точка A пройдет весь путь окружности, проекция этого пути равна диаметру описанной окружности. Так как точка O лежит на отрезке AT, то пройденный путь пропорционален диаметру описанной окружности с тем же коэффициентом пропорциональности, что и отношение отрезка OT к соответствующему пути. Получили, что искомое отношение радиусов равно отношению 
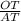. Пусть MB = x, AM = 3x; AN = 3y; NC = y; TC = BT; По теореме Менелая: 
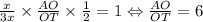, Значит 
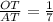; ответ: 7:1
Пошаговое объяснение:
64 мин. Из пункта А в пункт Б велосипедист вышел. Через 48 минут от точки А за ним поехал мотоциклист и прибыл в точку Б одновременно с велосипедистом. Сколько минут велосипедист находился в дороге, если известно, что его скорость в четыре раза меньше скорости мотоциклиста. Расстояние между A и B не указано, возьмем 1. 48 минут = 48/60 часов = 4/5 часов. Формула движения: S = v * t S- расстояние t - время y - скорость X - скорость велосипедиста. 4х - скорость мотоциклиста. 1 / x - время в пути велосипедиста. 1 / 4x - время мотоциклиста.1 / x = 1 / 4x TOTAL FRIEND 5 * 4x = 20x, перезаписать числа Дополнительные множители, избавиться от дробей: 20 * 1 = 5 * 1 + 4x * 4 20 = 5 + 16x 16x = 15 x = 15/16 ( км / час) - скорость велосипедиста. 15/16 * 4 = 15/4 (км / ч) - Скорость мотоциклиста. 1: 15/16 = 16/15 (час) - время в пути велосипедиста. В минутах: 16/15 * 60 = 64 (минуты). Чтобы узнать время мотоциклиста: 1: 15/4 = 4/15 (часы) = 16 (минуты). Вышло за 48 минут: 48 + 16 = 64 (минуты).64 = 64 Решение верное.
цена книги - цена тетради >100 руб
кол-во книг - кол-во тетрадей = 5
Найти: сколько книг куплено?
Решение:
1) Раз книги ПО ОДИНАКОВОЙ И ЦЕЛОЙ цене, то разложим их общую стоимость на простые множители
1071 = 3*3*7*17
2) количество книг НЕ МОЖЕТ БЫТЬ МЕНЬШЕ, т.к. их на 5 больше, чем тетрадей,т.е. хотя бы одна тетрадь должна быть, т.е. множитель 3 - не число книг.
3) количество книг должно быть МЕНЬШЕ 17, так как, если книг 17, то их стоимость получится 63 рубля, Это противоречит условию,т.к. книга должна быть, по крайней мере, на 100 рублей дороже тетради (Или: 1071:101=10,6, не больше 10 книг. Отбрасываем 23*7=21, 3*117 =51 и т.д)
4) Если куплено 7 книг, то цена каждой: 1071:7 = 153 рубля,
можно купить две тетради по цене менее 52 рублей. Не противоречит условию.
5) если куплено 3*3 = 9 книг, то их цена 1071:9 = 119 рублей, тогда куплено 4 тетради по цене менее 18 рублей.
6) поскольку других ограничений в условии нет, то можно было купить или 7, или 9 книг.
ответ: 7 или 9 книг.