1. НОК (9, 12)
Раскладываем на простые множители:
9=3*3
12=2*2*3
Списываем разложение большего числа и добавляем 3. Получается 36.
НОК (9, 12) = 36
2. НОК (24, 16)
Раскладываем на простые множители:
24=2*2*2*3
16=2*2*2*2
Списываем разложение большего числа и добавляем 2. Получается 48.
НОК (24, 16) = 48
3. НОК (6, 8, 12)
Раскладываем на простые множители:
6=2*3
8=2*2*2
12=2*2*3
Списываем разложение большего числа и добавляем 2 из меньших. Получается 24.
НОК (6, 8, 12) = 24
4. НОК (40, 25)
Раскладываем числа на простые множители:
40=2*2*2*5
25=5*5
Списываем разложение большего числа и добавляем 5 из разложения 25. Получаем 200.
НОК (40, 25) = 200
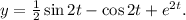
Пошаговое объяснение:
Имеем дело с неоднородным линейным уравнением с постоянными коэффициентами. Стандартный прием: искомое решение представляется в виде суммы решения однородного уравнения и частного решения неоднородного: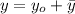 
.
Однородное уравнение: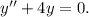 
Характеристическое уравнение имеет следующий вид: 
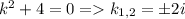. Тогда решение однородного уравнение можно записать в виде: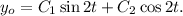 
Так как в правой части исходного уравнения перед экспонентой стоит многочлен нулевой степени, а коэффициент в показателе экспоненты не совпадает с каким-либо корнем характеристического уравнения, то частное решение можно искать в виде: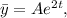 
подставим его в исходное уравнение и найдем коэффициент 
:
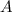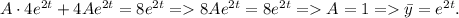
Значит, общее решение исходного уравнения есть
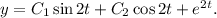Осталось определить коэффициенты для данной задачи Коши:
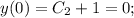
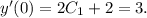
Решая каждое из этих уравнений, находим: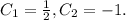 
В итоге, получаем ответ:
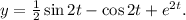
1) 35 деталей ➡ 100%
42 детали ➡ x %
35х = 4200
х = 4200 : 35
х = 120 (%)
2) 120 - 100 = 20 (%) перевыполнил
ответ : на 20% перевыполнил план