1)НОК ( 75; 60 ) = 300
Разложим числа на простые множители. Сначала запишем разложение на множители самого большого число, затем остальные числа. Подчеркнем в разложении меньших чисел множители, которые не вошли в разложение наибольшего числа.
75 = 3 · 5 · 5
60 = 2 · 2 · 3 · 5
Чтобы определить НОК, необходимо недостающие множители (эти множители подчеркнуты) добавить к множителям большего числа и перемножить их:
НОК (75; 60) = 3 · 5 · 5 · 2 · 2 = 300
2)НОК ( 12; 15; 20 ) = 60
20 = 2 · 2 · 5
12 = 2 · 2 · 3
15 = 3 · 5
Чтобы определить НОК, необходимо недостающие множители (эти множители подчеркнуты) добавить к множителям большего числа и перемножить их:
НОК (12; 15; 20) = 2 · 2 · 5 · 3 = 60
3)НОК ( 7; 11 ) = 77
11 – является простым числом
7 = 7
Чтобы определить НОК, необходимо недостающие множители (эти множители подчеркнуты) добавить к множителям большего числа и перемножить их:
НОК (7; 11) = 11 · 7 = 77
Пошаговое объяснение:
Изменение скорости автобуса можно представить в виде графика (смотрите ниже).
Тогда пройденный путь будет площадью прямоугольного треугольника (на чертеже выделен цветом), ограниченного в данном случае осью абсцисс, прямыми 
(м/с) и 
(с).
Для того, чтобы узнать его площадь, можно взять интеграл, как рекомендуется в задании:
Но можно ограничиться формулой площади прямоугольного треугольника (половина произведения длин катетов). Один катет которого равен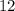 
, а другой - 
:
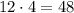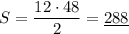
Но так или иначе, получаем, что автобусом будет пройдено 
метров.
17х–20х=8+7
–3х=15
х=15:(–3)
Х=–5
13Х+10=6х–4
13х–6х=–10–4
7х=–14
Х=–14:7
Х=–2
0.6(х–2)+4,6=0,4(7+х)
0.6х–1.2+4,6=2.8+0.4х
0.6х–0.4х=2.8+1.2
0.2х=4
Х=4:0,2
Х=20
13х+71–2=0
13х=–71+2
13х=–69
Х=–69:13
Х=–5.307