Да, всё правильно. Для n команд, число игр (при условии, что каждая команда играет одну игру с каждой командой соперников) равно сумме чисел от 1 до (n -1)
Задачу можно решить с наглядной иллюстрации:
обозначим точками команды, а линиями, которые их соединяют - игры.
Для 3-х команд получим треугольник, то есть 3 игры.
Для 4-х команд получим квадрат (4 стороны + 2 диагонали), то есть 6 игр.
Для 5-х команд получим 5-угольник (5 сторон + 5 диагоналей), то есть 10 игр, и т.д.
То есть искомое число игр есть сумма количества сторон и диагоналей 199-угольника.
Количество диагоналей n-угольника равно
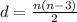
Количество сторон равно n
Находим сумму:
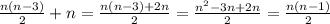
Подставим n=199 и получим:
199*198/2=19701
Известно, что середины сторон любого четырёхугольника являются вершинами параллелограмма. Значит ABCD– параллелограмм. Значит, О – середина BD.
Поскольку АО – медиана треугольника ABD, то площади треугольников АОKи АОLравны. Так как площади четырехугольников ALBOи AKDO тоже равны (=6), то и площади треугольников KOAи LOB равны. Основания этих треугольников равны (DO=OB, так как АС и BD точкой пересечения О делятся пополам), значит равны и их высоты, опущенные на эти основания. Отсюда KL|| BD.
Так как Dи В – середины отрезков LMи KN, то NM|| KL.Значит KLBD и DBMN– трапеции. Так как О и С – середины оснований трапеции DBMN, то площади DOCNи MCOBравны. Итак, площадь четырехугольника MCOB = 9.
б) 24\100= 6\25