1.
а) –2 < 5; б) –6 > –7; в) 2,5 > - 2,5; г) 3 > –1,5;
д) 36,5 > 0; е) –8,2 < 0; ж) 6,2 > 6,12; з) 0, 149 < 0,6
2.
а) 1,4 + 4,12=5,52
б) (–7) + (+3,6)= -3,4
в) –7 + 23=16
г) 2,6 + (–1,1)=1,5
д) (–4,9) + (–1,1)= -6
е) –3 + 3=0
3.
а) 6,37– (–14,1)=20,47
б) 2,66 –1,14=1,52
в) –7,44 – (–43,6)=36,16
г) – 4,09 –1,71= - 5,8
д) –7– 2= -9
е) –3 – 7= -10
4.
1) -(-3)· 5 = 15
2) -6:1= -6
3) -0,5∙(-0,9) = 0,45
4) -2,8 : 7= -0,4
5.
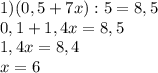
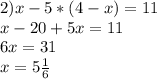
6.
8<9<12
8<10<12
8<11<12
ответ 9,10,11
Пошаговое объяснение:
Приведение к стандартному виду:
\begin{gathered}\displaystyle 2,\!1 \cdot a^2 b^2 c^4 \cdot \bigg ( - 1\frac{3}{7} \bigg ) \cdot bc^3 d = - \bigg ( \frac{21}{10} \cdot \frac{10}{7} \bigg ) \cdot a^2 \cdot b^2b \cdot c^4c^3 \cdot d = = - \frac{21}{7} \cdot a^2 \cdot b^{2+1} \cdot c^{4+3} \cdot d = \boxed {- 3a^2 b^3c ^7d}\end{gathered}2,1⋅a2b2c4⋅(−173)⋅bc3d=−(1021⋅710)⋅a2⋅b2b⋅c4c3⋅d==−721⋅a2⋅b2+1⋅c4+3⋅d=−3a2b3c7d
Коэффициент одночлена: \boxed {-3}−3 .
Задание 2.
Формула для нахождения объема прямоугольного параллелепипеда (VV - объем; xx , yy , zz - измерения прямоугольного параллелепипеда): V=xyzV=xyz .
Значит, объем исходного параллелепипеда равен:
\begin{gathered}V = \Big (4a^2b^5 \Big ) \cdot \Big (3ab^2 \Big ) \cdot \Big (2ab \Big ) = \Big (4 \cdot 3 \cdot 2 \Big ) \cdot a^2aa \cdot b^5b^2b = = 24 \cdot a^{2+1+1} \cdot b^{5+2+1} =\boxed {24a^4b^8}\end{gathered}V=(4a2b5)⋅(3ab2)⋅(2ab)=(4⋅3⋅2)⋅a2aa⋅b5b2b==24⋅a2+1+1⋅b5+2+1=24a4b8
S6=1,9(729-1)/2=1,9×364=691,6