Решить : в первом катере количество людей больше в 3 раза, чем во втором. если на пристани вышли из первого катера 20 человек, а на второй сели то же количество людей, то в обоях катера будет одинаковое количество людей. сколько людей было сначала в обоях катерах?

👇

Ответ:

regina290402

26.10.2020

Решим системой, где х - кол-во людей на первом катере, а у - на втором
х = 3у
х-20 - на у+20

Во втором уравнении заменим х на 3у и получим:
3у-20=у+20
3у-у=20+20
2у=40
у=20 - столько человек было на 2 катере
А так как в первом было в 3 раза больше, то на нем было 60 человек

4,4(61 оценок)

Открыть все ответы

Ответ:

Sasha190507

26.10.2020

Найдем сначала общее решение соответствующего однородного уравнения:

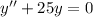
y''+25y=0

Пусть $y=e^{kx}$ , получим характеристическое уравнение:

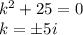
$k^2+25=0\\ k=\pm5i$

Характеристическое уравнение имеет два комплексных корня Два линейно независимые решения это 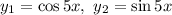$y_1=\cos 5x,~ y_2=\sin5x$

Общее решение однородного дифференциального уравнения:

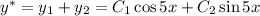
$y^*=y_1+y_2=C_1\cos 5x+C_2\sin5x$

Рассмотрим правую часть дифференциального уравнения:

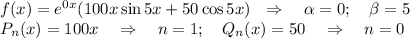
$f(x)=e^{0x}(100x\sin5x+50\cos 5x)~~\Rightarrow~~~\alpha =0;~~~ \beta=5\\ P_n(x)=100x~~~\Rightarrow~~~ n=1;~~~ Q_n(x)=50~~~\Rightarrow~~~ n=0$

Число 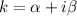$k=\alpha +i\beta$ принимает значение 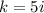k=5i , это число является корнем характеристическое уравнение 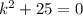k^2+25=0 . Кратность k=1

Частное решение будем искать в виде:

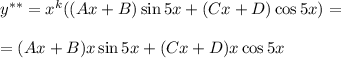
$y^{**}=x^{k}((Ax+B)\sin 5x+(Cx+D)\cos 5x)=\\ \\ =(Ax+B)x\sin 5x+(Cx+D)x\cos 5x$

Вычислим для нее производную второго порядка

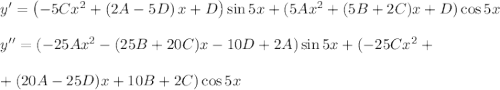
$y'=\left(-5Cx^2+\left(2A-5D\right)x+D\right)\sin 5x+(5Ax^2+(5B+2C)x+D)\cos5x\\ \\ y''=(-25Ax^2-(25B+20C)x-10D+2A)\sin 5x+(-25Cx^2+\\ \\ +(20A-25D)x+10B+2C)\cos 5x$

Подставив в исходное дифференциальное уравнение, получим:

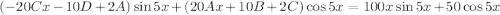
$(-20Cx-10D+2A)\sin 5x+(20Ax+10B+2C)\cos 5x=100x\sin 5x+50\cos5x$

Приравниваем коэффициенты при xcos5x, xsin5x, sin5x, cos5x, получим систему уравнений:

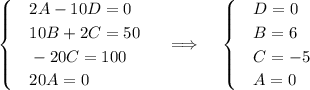
$\begin{cases}&\text{}2A-10D=0\\&\text{}10B+2C=50\\&\text{}-20C=100\\&\text{}20A=0\end{cases}~~~~\Longrightarrow~~~\begin{cases}&\text{}D=0\\&\text{}B=6\\&\text{}C=-5\\&\text{}A=0\end{cases}$

Частное решение: 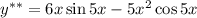$y^{**}=6x\sin 5x-5x^2\cos 5x$

Общее решение линейного неоднородного дифференциального уравнения:

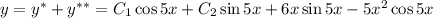
$y=y^*+y^{**}=C_1\cos 5x+C_2\sin5x+6x\sin 5x-5x^2\cos 5x$

4,5(8 оценок)

Ответ:

Настіяа

26.10.2020

Единая государственная система предупреждения и ликвидации чрезвычайных ситуаций (РСЧС): Единая государственная система предупреждения и ликвидации чрезвычайных ситуаций (РСЧС) создана с целью объединения усилий органов государственного управления всех уровней, подчиненных им сил и средств для предупреждения и ликвидации чрезвычайных ситуаций.
На каждом уроне единой системы создаются координационные органы, постоянно действующие органы управления, органы повседневного управления, силы и средства, резерв финансовых и материальных ресурсов, системы связи, оповещения и информационного обеспечения.
Координационными органами единой системы являются:: на федеральном уровне – Правительственная комиссия по предупреждению и ликвидации ЧС и обеспечению пожарной безопасности, комиссии по предупреждению и ликвидации ЧС и обеспечению пожарной безопасности федеральных органов исполнительной власти

4,4(89 оценок)

Это интересно:

Компьютеры-и-электроника

19.12.2022

Как отключить автозагрузку приложений на Android...

Питомцы-и-животные

17.04.2023

Объемная кровать для собаки: сделай сам и порадуй своего питомца...

27.02.2021

Как изменить всю свою личность: советы от психологов...

Семейная-жизнь

23.06.2022