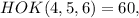
 где
где  – некоторое целое число.
– некоторое целое число.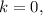 тогда
тогда 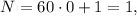 но
но  не делится на
не делится на  а значит не подходит.
а значит не подходит.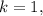 тогда
тогда 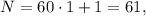 но
но 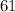 не делится на
не делится на  а значит не подходит.
а значит не подходит. тогда
тогда 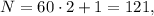 но
но 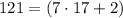 не делится на
не делится на  а значит не подходит.
а значит не подходит.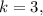 тогда
тогда 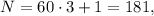 но
но 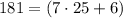 не делится на
не делится на  а значит не подходит.
а значит не подходит.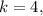 тогда
тогда 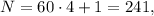 но
но 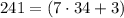 не делится на
не делится на  а значит не подходит.
а значит не подходит. тогда
тогда 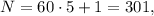 и
и 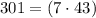 – делится на
– делится на  а значит подходит !
а значит подходит !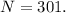
 где
где  – некоторое целое число.
– некоторое целое число.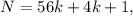 где
где  – некоторое целое число.
– некоторое целое число.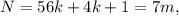 где
где  и
и 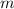 – некоторые целые числа.
– некоторые целые числа.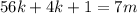 ;
;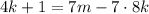 ;
;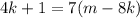 – правая часть здесь кратна семи, а значит и левая кратная семи, т.е.:
– правая часть здесь кратна семи, а значит и левая кратная семи, т.е.: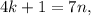 где
где  и
и  – некоторые целые числа.
– некоторые целые числа.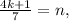 где
где  и
и  – некоторые целые числа.
– некоторые целые числа. а значит:
а значит: где
где 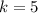 ;
;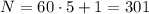 ;
; где
где  – некоторое целое число.
– некоторое целое число.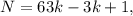 где
где  – некоторое целое число.
– некоторое целое число. где
где  и
и 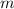 – некоторые целые числа.
– некоторые целые числа.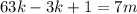 ;
;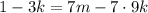 ;
;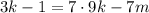 ;
;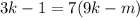 – правая часть здесь кратна семи, а значит и левая кратная семи, т.е.:
– правая часть здесь кратна семи, а значит и левая кратная семи, т.е.: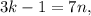 где
где  и
и  – некоторые целые числа.
– некоторые целые числа.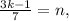 где
где  и
и  – некоторые целые числа.
– некоторые целые числа. а значит:
а значит: где
где 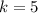 ;
;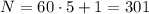 ;
;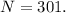
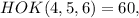
 где
где  – некоторое целое число.
– некоторое целое число.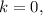 тогда
тогда 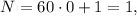 но
но  не делится на
не делится на  а значит не подходит.
а значит не подходит.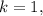 тогда
тогда 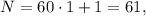 но
но 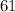 не делится на
не делится на  а значит не подходит.
а значит не подходит. тогда
тогда 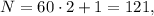 но
но 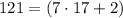 не делится на
не делится на  а значит не подходит.
а значит не подходит.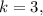 тогда
тогда 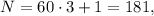 но
но 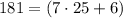 не делится на
не делится на  а значит не подходит.
а значит не подходит.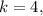 тогда
тогда 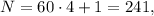 но
но 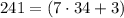 не делится на
не делится на  а значит не подходит.
а значит не подходит. тогда
тогда 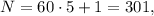 и
и 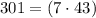 – делится на
– делится на  а значит подходит !
а значит подходит !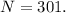
 где
где  – некоторое целое число.
– некоторое целое число.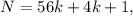 где
где  – некоторое целое число.
– некоторое целое число.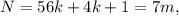 где
где  и
и 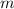 – некоторые целые числа.
– некоторые целые числа.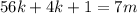 ;
;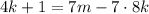 ;
;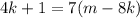 – правая часть здесь кратна семи, а значит и левая кратная семи, т.е.:
– правая часть здесь кратна семи, а значит и левая кратная семи, т.е.: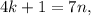 где
где  и
и  – некоторые целые числа.
– некоторые целые числа.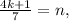 где
где  и
и  – некоторые целые числа.
– некоторые целые числа. а значит:
а значит: где
где 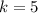 ;
;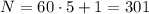 ;
; где
где  – некоторое целое число.
– некоторое целое число.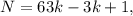 где
где  – некоторое целое число.
– некоторое целое число. где
где  и
и 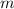 – некоторые целые числа.
– некоторые целые числа.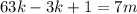 ;
;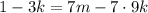 ;
;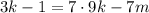 ;
;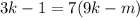 – правая часть здесь кратна семи, а значит и левая кратная семи, т.е.:
– правая часть здесь кратна семи, а значит и левая кратная семи, т.е.: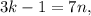 где
где  и
и  – некоторые целые числа.
– некоторые целые числа.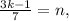 где
где  и
и  – некоторые целые числа.
– некоторые целые числа. а значит:
а значит: где
где 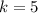 ;
;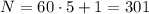 ;
;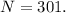
Чтобы найти k и b, решим систему уравнений, где (х; у) это координаты точек А(1; 5) и В(-1; 1)
{1·k + b = 5
{- 1·k + b = 1
Сложив эти уравнения, получим
k + b - k + b = 5 + 1
2b = 6
b = 6 : 2
b = 3
Подставим b = 3 в первое уравнение k + b = 5 и найдём k.
k + 3 = 5
k = 5-3
k = 2
Подставим k = 2 и b = 3 в уравнение прямой у = kх + b:
у = 2х +3 получили искомое уравнение прямой.
ответ: у = 2х + 3