Решение.
Объем пирамиды найдем по формуле:
V=1/3 Sh
Зная диагональ основания пирамиды, найдем сторону основания.
d2 = a2 + a2
42 = 2a2
16 = 2a2
a= √8 = 2√2
Соответственно, площадь основания
S = 8 см2 .
Проведем через вершину правильной четырехугольной пирамиды вертикальное сечение. Поскольку боковые грани пирамиды наклонены к основанию под углом 60 градусов, то сечение образует равносторонний треугольник.
Основание равностороннего треугольника равно 2√2. Откуда высота будет равна
h = √3/2 a
h = √3/2 * 2√2 = √6
Откуда объем правильной пирамиды с четырехугольником в основании равен
V=1/3 Sh
V = 1/3 * 8 * √6 = 8√6 / 3
ответ: 8√6 / 3 см3.
ответ: 7π
Пошаговое объяснение:
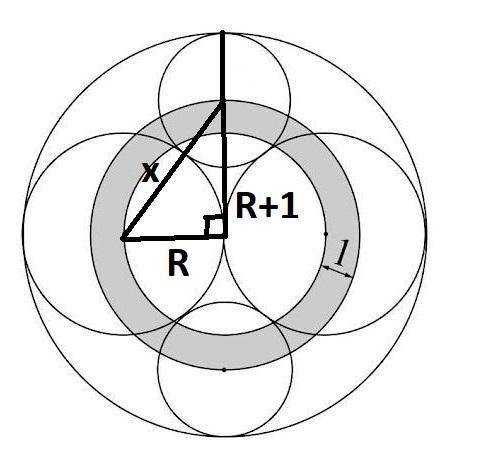
Пусть радиус окружности внутри кольца равен R, в снаружи R+1, соответственно, а расстояние от центра малой окружности до центра большей окружности равно x (из четырех окружностей ,касающихся внутренним образом cамой большой окружности), тогда радиус самой большой окружности можно определить двумя :
2R или R+1 + x - R = x+1, то есть
2R = x+1
x = 2R-1
x^2 = (2R-1)^2
По теореме Пифагора:
x^2 = R^2 + (R+1)^2
Откуда:
R^2 + (R+1)^2 = (2R-1)^2
2R^2 -6R = 0
R≠0
R - 3 = 0
R = 3
Площадь кольца:
S = π( (R+1)^2 - R^2) = π(4^2 - 3^2) = 7π
Значит и дочери в 2-е больше:
8*2=16-лет дочке.