ответ:13860
Пошаговое объяснение:1. Раскрасим основание A1A2...A4 в один из 11 цветов. Такую раскраску можно осуществить
2. Раскрасим теперь по очереди боковые грани пирамиды. Для первой грани SA1A2 имеется 11−1=10 вариантов раскраски, для второй грани SA2A3 имеется 11−2=9 вариантов раскраски, и так далее, для 4-й по порядку грани имеется 11−4=7 вариант(-ов, -a) раскраски. Таким образом, всего получаем
M=11(11−1)(11−2)...(11−4)
вариантов раскраски пирамиды.
3. По условию задачи две раскраски считаются одинаковыми, если получаются друг из друга движением. В нашем случае, у пирамиды существует ровно 4 движений (4 поворотов). Потому искомое число раскрасок будет в 4 раз меньше величины M.
Получаем ответ:
11(11−1)(11−2)...(11−4)4=13860.
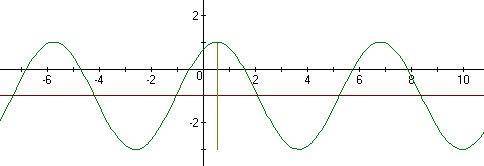
Обычная косинусоида при x=0 имеет y=+1. Период 2 Пи =6.28. отложите его на оси.
Сдвиг по фазе -30 градусов означает сдвиг всей кривой вправо на 1/6 полупериода или 1/12 периода (это чуть больше 0,5). отложите метки на оси.
Коэффициент 2 растягивает результат по вертикали симметрично, а сдвиг -1 сдвигает вниз на 1.
Окончательно кривая лежит между горизонталями +1 и -3
Реально надо бы рассчитать точку сдвига, помеченную крестом, и относительно неё строить с обычным периодом растянутую по вертикали косинусоиду.
Этот процесс нужно только для понимания как строится такая кривая.
А практически, вычисляем таблицу по формуле с малым шагом, откладываем точки на графике и соединяем плавно.
Пошаговое объяснение:
с=154-83
b=49+91
d=540-370
х=960/4
R=400:80