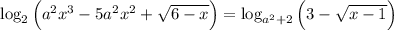
Раз некоторое число 
удовлетворяет уравнению при любом 
, то оно также удовлетворяет уравнению при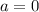 
.
То есть, если мы подставим в уравнение 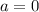, то выполнится равенство:
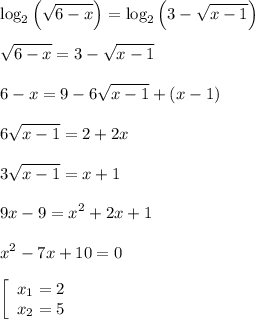
Оба корня удовлетворяют уравнению и ОДЗ (при 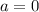): с обеих сторон в первом случае получается 
, а во втором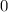 
(так как мы не выписывали ОДЗ, то мы могли получить "лишние корни", но мы их не получили).
Очевидно, что эти два корня в ответ так сразу не пойдут. Мы знаем лишь только, что они подходят при 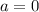. И если ответ на задачу существует, то он может быть только 
, 
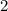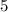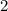или и , и 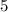. Но про другие значения мы пока ничего не знаем.
Посмотрим, что у нас будет получаться при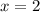 
:
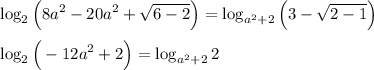
Вот только первый логарифм не всегда существует.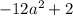 
может быть отрицательным (возьмите, к примеру, 
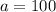). А подлогарифмическое выражение обязано быть положительным. Значит, такой нас не устраивает.
Теперь проверим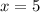 
:
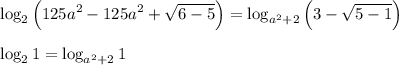
В обеих частях мы получили 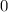(так как 
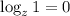, если 
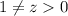). Также 
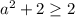, поэтому все ограничения будут выполняться.
В итоге имеем нужный ответ: .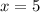
Задача решена!
Пошаговое объяснение:
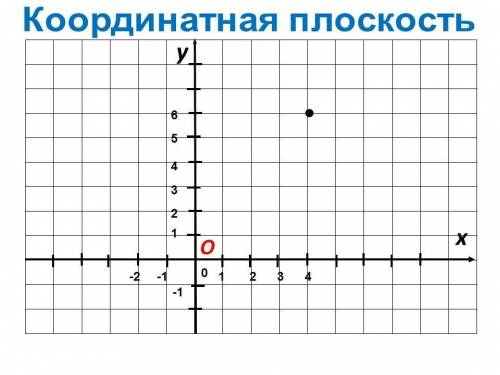
Ну смотри, строим координатную плоскость. Я ниже прикрепила картинки общего вида координатной плоскости и где какая четверть. Тебе нужно поставить точку А(-1; -2). У тебя на координатной плоскости есть цифры. Вправо - значения аргумента (х) со знаком плюс, влево - значения аргумента (х) со знаком минус. Вверх - значение ординаты (y) со знаком плюс, вниз - ординаты (y) со знаком минус. Есть точка А. В скобках написаны значения х (-1) и y (-2). Находишь на координатной плоскости по оси х число -1, от этой цифры ведёшь пальцем вертикально вниз до числа -2 по оси y. И ставишь точку и рядом букву А. Всё, по такому принципу остальные точки. На первой картинке внизу показан пример, как ставить точку с координатой (4; 6). Думаю понятно
