ответ: Запишем с пом. цифр 3 и 5 четыре двузначных числа: 35, 53, 33 и 55. Несмотря на то что числа 35 и 53 записаны с одних и тех же цифр, эти числа различные. В том случае, когда важен порядок следования элементов, в математике говорят об упорядоченных наборах элементов. В рассмотренном примере мы имели дело с упорядоченными парами.
Упорядоченную пару, образованную из элементов а и Ь, принято записывать, используя круглые скобки: <а; Ь). Элемент а называют первой координатой (компонентой) пары, а элемент b второй координатой (компонентой) пары.
Саму задачу можно переформулировать немного по-другому:
Было: Расставить минимальное количество шашек на шахматной доске 8 на 8, так чтобы было невозможно поставить коня так, чтобы он не бил ни одной шашки.Переходит в: расставить на доске минимальное количество коней так, чтобы было невозможно поставить шашку не под удар коня.Если мы решим вторую задачу, то просто нужно будет заменить коней шашками - и мы получим искомое расположение.
По поводу второй задачи можно заметить, что:
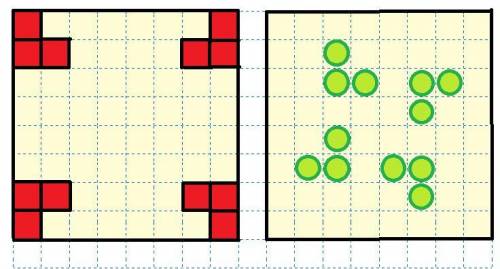
Разные кони должны бить выделенные красным клетки на рисунке ниже.Отсюда следует, что мы не можем расставить менее, чем 4 * 3 = 12 коней. Если это можно сделать, то задача решится. И да, это получилось сделать (рисунок 2).
Заменяем коней шашками и получаем ответ: 12 коней.
ответ: 12 шашек.
при двух бросках всего событий 6*6=36
Так как 36 относительно небольшое число вариантов, рассмотрим подробнее какие события благоприятные,
1, 1 (1*1=1<9) - благоприятное
1,2; 1,3; 1,4; 1,5; 1,6;
2,1; 2,2; 2,3; 2,4;
3,1;3,2;
4,1; 4,2;
5,1;
6,1;
всего 16
(неблагоприятные
2,5; 2,6; 3,3; 3,4; 3,5; 3,6; 4,3; 4,4; 4,5; 4,6; 5,2; 5,3; 5,4; 5,5; 5,6; 6,2; 6,3; 6,4; 6, 5; 6,6;)
Следовательно вероятность равна 16/36=4/9
ответ: 4/9