Боковые стороны трапеции равны по 8 см.
Пошаговое объяснение:
Трапеция называется равнобокой, если ее боковые стороны равны.
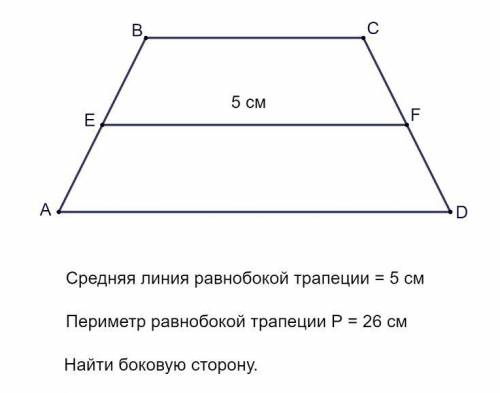
Пусть дана равнобокая трапеция ABCD. Ее боковые стороны равны AB = CD. Средняя линия EF = 5 см.
Средняя линия трапеции - это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции равна полусумме оснований.
EF =  см
см
BC + AD = 2 * 5 = 10 (см)
Периметр равен сумме длин всех сторон, P = 26 см.
Сумма боковых сторон трапеции: AB + CD = P - (BC + AD) = 26 - 10 = 16 (см).
Боковые стороны: AB = CD = 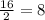 (см).
(см).
Пусть в один мешок помещается x кг картофеля или моркови. Тогда мешков с картофелем будет 350/x шт, с морковью - 960/x шт, что на 80 мешков больше, чем с картофелем. То есть:
Тогда, мешков с картофелем 350/7,625 ≈ 46,
мешков с морковью - 960/7,625 ≈ 126.
P.S. Округляем вверх, т.к. мешков может быть только целое число.