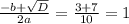
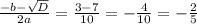
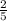
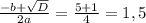
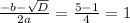
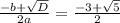
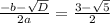
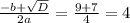
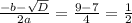
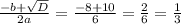
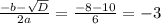
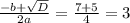
Пошаговое объяснение:
С одной стороны, ромб состоит из 2 равнобедренных треугольников, каждый из которых имеет боковую сторону а = 4,5 см и угол между ними А = С = 56 гр. Площадь треугольника можно вычислить так:
S(тр) = 1/2*a*a*sin 56 = 4,5^2/2*sin 56
Площадь ромба S = 2S(тр) = 4,5^2*sin 56 = 20,25*sin 56
С другой стороны, можно по теореме косинусов вычислить диагонали.
d1^2 = a^2 + a^2 - 2a*a*cos 56 = 2a^2(1 - cos 56) = 2a^2 * 2sin^2 28 (по формуле половинного аргумента sin x/2)
d1 = 2*4,5*sin 28 = 9*sin 28
d2^2 = a^2 + a^2 - 2a*a*cos (180 - 56) = 2a^2(1 + cos 56) = 2a^2 * 2cos^2 28 (по такой же формуле cos x/2)
d2 = 2*4,5*cos 28 = 9*cos 28
Площадь ромба равна половине произведения диагоналей.
S = d1*d2/2 = 9*sin 28 * 9*cos 28 / 2 = 40,5*sin 28*cos 28 = 20,25*2*sin 28*cos 28 = 20,25*sin 56
(по формуле двойного аргумента sin 2x)
D=9+40= 49
x(1,2) = 3+-7/10= 1;-0,4
2x^2 - 5x+3=0
D= 25-24=1
x(1,2) = 5+-1/4= 1; 3/2
x^2+3x+1=0
D= 9-4= 5;
x(1,2) = -3+-√5/2 = 0,5(-3+√5); 0,5 (-3-√5)
2x^2-9x+4= 0
D= 81-32= 49;
x(1,2) = 9+-7/4= 4;1/2
11x-3= 0
x= 3/11
-5x+3=0
x= 3/5