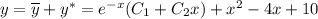Классическая вероятность события:
,
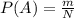где P(A) — вероятность события A;
m — число благоприятных событий;
N — число всех возможных событий.
1) событие A — книга будет на эстонском, m — 6, N — 6+4=10
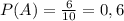
2) событие A₁ — книга с 1-й полки будет на эстонском, m — 6, N — 6+4=10
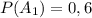
событие B₁ — книга со 2-й полки будет на эстонском, m — 5, N — 5+3=8
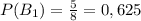
Произведение совместных событий:
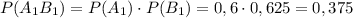
событие A₂ — книга с 1-й полки будет на английском:
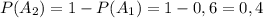
событие B₂ — книга со 2-й полки будет на английском:
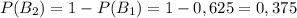
Произведение совместных событий:
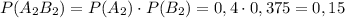
Сумма совместных событий:
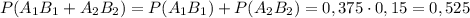
1) 0,6 или 60% ;
2) 0,525 или 52,5%
Найдем начала общее решение соответствующего однородного дифференциального уравнения
(*)
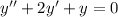Воспользовавшись заменой Эйлера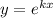 
, мы получим характеристическое уравнение
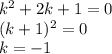
Общее решение уравнения (*)
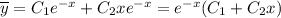
Далее нужно найти частное решение. Рассмотрим функцию:
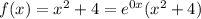
Здесь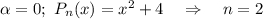 
Сравнивая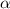 
с корнями характеристического уравнения и, принимая во внимая, что 
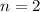частное решение будем искать в виде
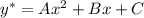
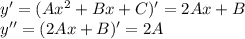
Подставляем все это в исходное дифференциальное уравнение
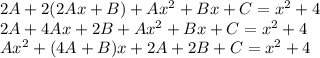
Приравниваем коэффициенты при степени x
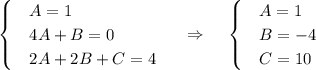
Частное решение: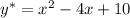 
Общее решение линейного неоднородного дифференциального уравнения:
