Вот решение лови картинку
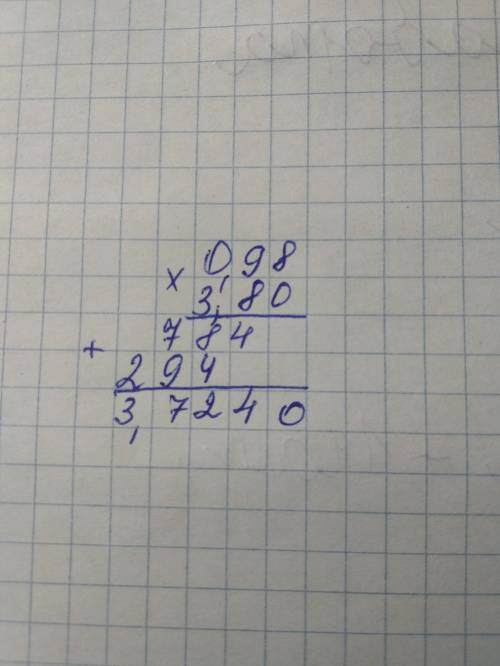
1)Вычислить угол между прямыми:
3x+2y-7=0
2x-3y+9=0
найдём угловые коэффициенты заданных прямых:
2у = 7 - 3х
3у = 2х + 9
дальше:
у = 7/2 - 3/2 х
у = 3 + 2/3 х
угловые коэффициенты прямых: k1 = -3/2, k2 = 2/3
Прямые перпендикулярны, если их угловые коэффициенты удовлетворяют соотношению k1 = -1/k2.
В нашем случае как раз: -3/2 = - 1/ (2/3)
ответ: Угол между прямыми равен 90 градусам.
2)Составить уравнение прямой, проходящей через точку Mo, перпендикуларно П(над символом проведена черта).
Mo(3;-2); П=(3;-2)
По проекциям вектора П можно вычислить угловой коэффициент прямой, его содержащей: k1 = -2/3. Тогда угловой коэффициент перпендикулярной прямой:
k2 = -1/k1 = 3/2
Ищем прямую у = k2·х + b или у = 3/2·х + b, проходящую через точку Мо. имеющую координаты х = 3, у = -2. подставим эти значения в уравнение прямой и найдём b.
-2 = 3/2·3 + b
b = -2 - 4.5 = -6.5
Итак, искомое уравнение прямой
у = 1,5х - 6,5
28-(-3 5/12)+(-4 23/30-2 1/4)=24,4
1) -4 23/30-2 1/4 = -4 46/60 - 2 15/60 = -7 1/60
2) 28-(-3 5/12)= 28 + 3 5/12 = 31 5/12
3) 31 5/12 + (-7 1/60) = 31 25/60 - 7 1/60 = 24 24/60 = 24 2/5
4,6-1 11/15-(-2,3+5 1/3)= -1/30
1) -2,3+5 1/3 = - 2 3/10 + 5 1/3 = -2 9/30 + 5 6/30 = 2 27/30 = 2 9/10
2)4,6-1 11/15 = 4 6/10 - 1 11/15 = 4 18/30 - 1 22/30 = 2 26/30
3) 2 26/30 - 2 9/10 = 2 26/30 - 2 27/30 = - 1/30
-1 2/3×3,4×(-2 2/17)=2 11/17
1)-1 2/3×3,4 = -5/3 • 3/4 = -5/4 = -1 1/4
2) -1 1/4×(-2 2/17)=-5/4 • (-36/17) = -5/1 • (-9/17) = 45/17 = 2 11/17
1 9/31×(-3,1)×(-17,75)=71
1) 1 9/31×(-3,1) = 40/31 • (-31/10) = -4
2) -4/1 • (-1775/100) = -1/1 • (-1775/25) = 1775/25 = 71
0,98
х
3,8
———
3,724