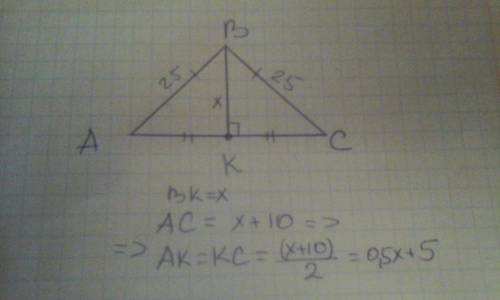
Вывод: АК = КС = (х+10):2= 0,5х+5
Рассмотрим треугольник ВКС-прямоугольный
х² + (0,5х+5)²=25² - теорема Пифагора (квадрат гипотенузы = сумме квадратов катетов)
х² + (0,25х²+5х+25)-25²=0
1,25х²+5х+25-625=0
1,25х²+5х-600=0 - квадратное уравнение
Д=5² -4*1,25*(-600)=25 + 3000=3025 =55²
х₁ = (-5 - √3025):(1,25*2)= -60: 2,5= - 24 -корень не подходит
х₂ = (-5 + √3025):(1,25*2)=50: 2,5= 20 см -высота ВК
АС=(х+10)=20+10=30 см - основание
S= 1/2 *АС*ВК = 1/2 *30*20=300см² - площадь треугольника АВС
Р=АВ+АС+ВС=25+30+25=80см - периметр треугольника
2019
Пошаговое объяснение:
Первое число было трёхзначным, второе - четырёхзначным, т.к. и с лишним нулём, и без него ответ получился четырёхзначным и больше 2000.
* * * 0
* * * *
7059
Последняя цифра второго числа получается 9. Подставим её в правильное решение. Получим, что последняя цифра первого числа 4.
Раскручиваем далее. Т.к. предпоследняя цифра ответа 2, и единицу мы переносили от 4+9, то предпоследняя цифра первого числа 0.
* * * * * 4 *04
* * * 9 * * 1 9 * * 19
2523 2523 2523
Полученные цифры подставляем в неправильный пример. Т.к. к нулю прибавляем что-то и получаем снова 0, то предпоследняя цифра второго числа тоже 0.
* 040 * 040
* *19 *019
7059 7059
Полученные цифры подставляем в правильный пример. Т.к. вторая цифра ответа 5 получена сложением 0 и чего-то, то первая цифра первого числа 5. Значит, первая цифра второго числа 2
*04 504 504+2019 = 2523, 5040+2019= 7059
* 019 *019
2523 2523
1. Обозначим искомый угол DAC как b (естественно лучше использовать греческие буквы, я для простоты возьму латинские), а угол AFC = BFC как a. Соответсвенно углы AFB и CFD будут равны 180 - a (буду использовать для измерения углов градусы, но можно и в радианы перевести, конечно).
2. Распишем известные нам площади треугольников через две стороны и синус угла между ними. Сразу все не будем, по порядку:
Safb = 40 = 1/2 * BF * AF * sin (180 - a)
Вспомним, что sin (180 - a) равен sin a:
Safb = 40 = 1/2 * BF * AF * sin a
Теперь выпишем для следующего треугольника:
Sbfc = 80 = 1/2 * BF * 16 * sin a
А теперь мы видим, что эти выражения очень похожи. В них три неизвестных, но если одно выражение поделить на другое, то два из неизвестных уйдут:
80/40 = (1/2 * BF * 16 * sin a) / (1/2 * BF * AF * sin a)
2 = 16 / AF
AF = 8
Мы нашли AF и соответственно можем утверждать, что вся диагональ AC равна: AC = AF + FC = 8 + 16 = 24
3. Теперь рассмотрим ещё два треугольника и тоже применим для них такое выражение для площади:
Safd = 1/2 * AF * AD * sin b = 1/2 * 8 * 30 * sin b = 120 sin b
Второй треугольник ACD. Заметим, что он состоит из треугольников AFD и CFD, иными словами:
Sacd = Safd + Scfd = Safd + 120
А теперь запишем его площадь через синус, но вместо площади подставим предыдущую строчку:
Sacd = Safd + 120 = 1/2 * AC * AD * sin b
Safd + 120 = 1/2 * 24 * 30 * sin b = 360 sin b
Подставляя полученное чуть раньше Safd = 120 sin b, получаем:
120 sin b + 120 = 360 sin b
120 = 240 sin b
sin b = 1/2
Как мы знаем, синус 1/2 бывает у углов в 30 или 150 градусов, или, если выражаться корректнее и в радианах, (