11
Пошаговое объяснение:
В задаче учитывают только дома, стоящие на каком-то отрезке улицы.
Пусть пропустили первые n домов с нечетными номерами, а учли k домов. Известно, что сумма первых x нечетных чисел равна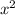 
, так что сумма всех номеров учтенных домов = сумма номеров первых n + k домов с нечетными номерами - сумма номеров первых n номеров с нечетными номерами =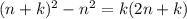 
Первый сомножитель явно меньше второго, и так как есть только два разложения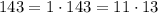 
, то и возможных вариантов ответа только два: k = 1 (то есть там стоит только один дом с номеров 143) либо k = 11 (тогда n = 1 и на улице стоят дома с номерами 3, 5, 7, ..., 23)
Изначально у друзей было 24 и 8 монет.
Пошаговое объяснение:
Задачу можно решить методом итераций.
1. Обозначим А - количество монет у первого пирата через два дня (в нашем случае А=18 ).
Обозначим В - количество монет у второго пирата через два дня (в нашем случае В = 14).
За день до этого у пиратов было a и b монет, соответственно. Найдем a и b решив систему уравнений. Согласно условиям,
A = a/2 + (a/2 + b/2)/2
B = b/2 + (a/2 + b/2)/2
Решив эту систему получим:
a = (3A - B) / 2
b = (3B - A) / 2 (система уравнений 1)
Подставляя А = 18 и В = 14, из системы (1) получим:
a = 20
b = 12
Таким образом, за день до второго дня (т.е. через день после начала перераспределения монет) у пиратов было 20 и 12 монет, соответственно.
Теперь повторим итерацию. Это значит, что через день после начала перераспределения монет у пиратов было 20 и 18 монет. Положим А = 20 и В = 18. Тогда в первый день, до начала перераспределения монет, у пиратов было a и b монет, соответственно. Найдем a и b из уравнений системы (1), положив А = 20 и В = 12. Получим:
a = 24
b = 8
Таким образом, в первый день, изначально у пиратов было: у одного 24 монеты, у другого 8 монет.
15/x=5/3
45=5x
x=9 (кг)
ответ: из 15 кг свежих ягод получится 9 кг сушёных.