Ну как бы не совсем то но буквы на свои поменяй и получится
Пошаговое объяснение:
Условие
Из вершины A треугольника ABC опущены перпендикуляры AM и AP на биссектрисы внешних углов B и C.
Докажите, что отрезок PM равен половине периметра треугольника ABC.
Подсказка
Пусть прямые AM и AP пересекают прямую BC в точках K и L. Тогда отрезок KL равен половине периметра исходного треугольника, а MP – средняя линия треугольника AKL.
Решение
Пусть прямые AM и AP пересекают прямую BC в точках K и L. Поскольку высоты BM и CP треугольников ABK и ACL являются их биссектрисами, то эти треугольники равнобедренные, поэтому BK = AB и CL = AC. Значит, отрезок KL равен периметру треугольника ABC.
Высоты BM и CP равнобедренных треугольников ABK и ACL являются их медианами, поэтому точки M и P – середины отрезков AK и AL. Значит, MP – средняя линия треугольника AKL. Следовательно, отрезок MP равен половине отрезка KL, то есть половине периметра треугольника ABC.
.
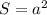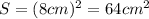, а площадь каждого маленького квадрата 
.
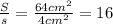. Итак, у Гриши из одного большого квадрата получилось 16 маленьких. Это ответ на первый вопрос.
, всего же в ряду, выложенном Гришей, 16 квадратов. Тогда длина ряда будет: 
. Это ответ на второй вопрос.
