-12,25;-12;30
Пошаговое объяснение:

А вот дальше тонкий момент. Если бы нас просили упростить, то можно было бы сократить скобки (x+2)(x-5), и осталось бы квадратное выражение.
Но у нас функция, в которой изначально эти две скобки стоят в знаменателе. Значит, по области определения, x ≠ -2 и x ≠ 5.
Это так называемые устранимые разрывы.
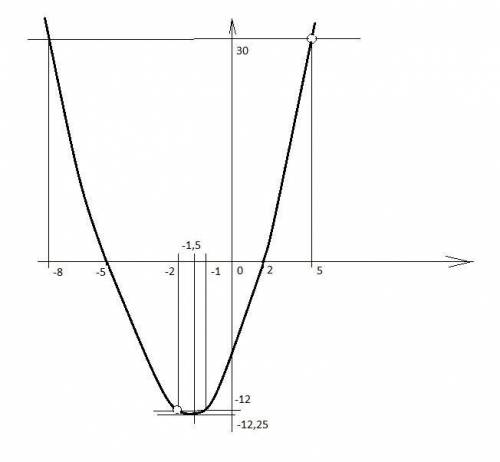
То есть графиком будет парабола y = x^2 + 3x - 10 с двумя выколотыми точками: x = -2; y = (-2)^2 + 3(-2) - 10 = -12 и x = 5; y = 5^2 + 3*5 - 10 = 30.
Значит, по 1 точке пересечения будут иметь прямые y = -12 и y = 30.
Они пересекаются с графиком в точках
x = -1; y = (-1)^2 + 3(-1) - 10 = -12 и x = -8; y = (-8)^2 + 3(-8) - 10 = 30.
Кроме того, у параболы еще есть вершина:
x0 = -b/(2a) = -3/2 = -1,5; y0 = (-1,5)^2 + 3(-1,5) - 10 = -12,25.
Значит, прямая y = -12,25 тоже имеет 1 точку пересечения с графиком.
Примерный график я нарисовал, но вы в тетради по клеточкам нарисуете лучше.
-12,25;-12;30
Пошаговое объяснение:

А вот дальше тонкий момент. Если бы нас просили упростить, то можно было бы сократить скобки (x+2)(x-5), и осталось бы квадратное выражение.
Но у нас функция, в которой изначально эти две скобки стоят в знаменателе. Значит, по области определения, x ≠ -2 и x ≠ 5.
Это так называемые устранимые разрывы.
То есть графиком будет парабола y = x^2 + 3x - 10 с двумя выколотыми точками: x = -2; y = (-2)^2 + 3(-2) - 10 = -12 и x = 5; y = 5^2 + 3*5 - 10 = 30.
Значит, по 1 точке пересечения будут иметь прямые y = -12 и y = 30.
Они пересекаются с графиком в точках
x = -1; y = (-1)^2 + 3(-1) - 10 = -12 и x = -8; y = (-8)^2 + 3(-8) - 10 = 30.
Кроме того, у параболы еще есть вершина:
x0 = -b/(2a) = -3/2 = -1,5; y0 = (-1,5)^2 + 3(-1,5) - 10 = -12,25.
Значит, прямая y = -12,25 тоже имеет 1 точку пересечения с графиком.
Примерный график я нарисовал, но вы в тетради по клеточкам нарисуете лучше.

(x-a)(x-b)+(x-b)(x-c)=0
(x-b)(x-a+x-c)=0
(x-b)(2x-(a+c))=0
(x-b)(x-(a+c)/2)=0
x-b=0
x₁=b
x-(a+c)/2=0
x₂=(a+c)/2
Значит сумма двух различных корней уравнения будет:
х₁+х₂=b+(a+c)/2
Если рассматривать различные четные числа из промежутка [5; 47], то это могут быть наименьшие последовательные числа - 6, 8, 10
Теперь найдем наименьшее значение суммы корней:
b=6
a=10
c=8
х₁+х₂=b+(a+c)/2=6+(10+8)/2=15
b=8
a=10
c=6
х₁+х₂=b+(a+c)/2=8+(10+6)/2=16
b=10
a=6
c=8
х₁+х₂=b+(a+c)/2=10+(6+8)/2=17
-
Очевидно, что наименьшее значение сумма корней уравнения будет равным 15
ответ 15