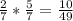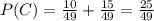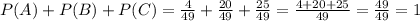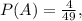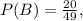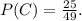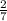Математика: Напряги мозги челлендж 135*1129+(550-40*30)-69

Напряги мозги челлендж 1351129+(550-4030)-69

👇

Увидеть ответ

Ответ:

danilcoptsov1

18.02.2021

= 152415+(-650)-69=151696

4,5(25 оценок)

Ответ:

Eva345678

18.02.2021

135×1129+(550−40×30)−69=151696
40×30=1200
550-1200=−650
135×1129=152415
152415+-650=151765
151765-69=151696

4,4(66 оценок)

Открыть все ответы

Ответ:

Липапит

18.02.2021

Что не будет ни одного выстрела.

Когда в первый раз крутим барабан и стреляем, получаем, что не выстрелит с вероятностью $\frac{2}{7}$ . Теперь снова крутим барабан и стреляем, получаем снова ту же вероятность 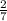$\frac{2}{7}$ . Так как барабан покрутили и выстрелы не были совершены подряд. Иначе вероятность с выстрелами подряд была бы иной. Значит эти вероятности перемножаются. Получаем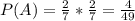

$P(A)=\frac{2}{7}*\frac{2}{7}=\frac{4}{49}$

Будет два выстрела.
Опять таки при прокрутке барабана получаем вероятность выстрела $\frac{5}{7}$ . Снова крутим барабан, стреляем с такой же вероятностью   $\frac{5}{7}$ . Выстрелы были совершены не подряд, поэтому такие вероятности.

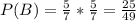
$P(B)=\frac{5}{7}*\frac{5}{7}=\frac{25}{49}$

Будет один выстрел

Рассмотрим два варианта
1) Крутится барабан и происходит выстрел.

Это происходит с вероятностью как уже было сказано $\frac{5}{7}$ . Но вот теперь патронов осталось четыре. И нужно, чтобы во второй раз уже не выстрелило. Значит после прокрутки барабана получаем вероятность невыстрела равную 3 из 7   $\frac{3}{7}$ .

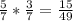
Эти два случая перемножаются и будет $\frac{5}{7}*\frac{3}{7}=\frac{15}{49}$

2) Крутится барабан и не происходит выстрел.

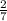Это будет как уже отмечали с вероятностью $\frac{2}{7}$ . Потом количество патронов осталось равное 5. Значит во второй раз после прокрутки барабана вероятность выстрела равна   $\frac{5}{7}$ .

Эти два случая тоже перемножаются, получается

   $\frac{2}{7}*\frac{5}{7}=\frac{10}{49}$

Вобщем

$P(C)=\frac{10}{49}+\frac{15}{49}=\frac{25}{49}$

Заметим, что P(A), P(B), P(C) - образуют полную вероятностную картину.

Так как $P(A)+P(B)+P(C)=\frac{4}{49}+\frac{20}{49}+\frac{25}{49}=\frac{4+20+25}{49}=\frac{49}{49}=1$

Значит задачу решили правильно. Так как при таком случае возможны только три исхода. А) два раза не стрелял, В) Два раза стрелял, С) самое вероятное: один раз выстрелил, а второй раз - нет.

ответ: $P(A)=\frac{4}{49},$ $P(B)=\frac{20}{49},$ $P(C)=\frac{25}{49}.$

4,6(97 оценок)

Ответ:

Nina34732

18.02.2021

Будем считать что есть три части флага, которыми могут стать полосы. Я понятно выразился? Так вот, в первую часть может превратиться одна из 5 полос. В вторую --- одна и оставшихся четырёх полос, а в третью -- одна и трёх оставшихся полос. Дальше перемножаем 5, 4 и 3, и получаем 60. Нам не всё равно в каком порядке стоят полосы, так как например "красный; синий; зелёный;" и "синий; зелёный; красный;" --- это разные флаги. Но если бы нам надо было посчитать сколько разных есть взять тройки полос, нам бы не имело значения в каком порядке они бы лежали, потому что "красный; синий; зелёный;" и "синий; зелёный; красный;"--- это одна тройка. И нам надо бы было поделить 60 (количество разных флагов) на количество разных в каком порядке разложить полосы, в нашем случае 6. И получилось бы: 60 / 6 = 10.
Это называется Бином Ньютона.

4,7(22 оценок)

Это интересно:

Дом-и-сад

23.11.2020

Как навести порядок в гараже: полезные советы от специалистов...

Кулинария-и-гостеприимство

04.04.2021

Как готовить только для себя: полезные советы и рецепты...

Кулинария-и-гостеприимство

11.11.2022

Сладкий рецепт: американские панкейки с нутеллой...

Кулинария-и-гостеприимство