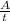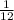) 
частей/год. Тогда второй выполняет тот же объем работ за 8 лет (A=1; t=8; 
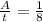) и третий за "x" лет (A=1; t=x; 
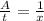). Из условия известно, что три насоса вместе справляются с работой за 4 года (A=1; t=4; 
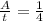). Значит общая производительность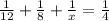
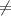0 ⇒ можем обе части уравнения умножить на одно и то же число (24x).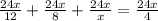
пусть число: 1000a + 100b + 10c + d
тогда
1000a + 100b + 10c + d + a + b + c + d = 1999
1001a + 101b + 11c + 2d = 1999
очевидно, что а = 1
101b + 11c + 2d = 998
b = 8 или b = 9
1) b = 8
11c + 2d = 190
99 + 18 < 190 - не подходит
2) b = 9
11c + 2d = 89
c = 7
2d = 12
d = 6
ответ: 1976