№1.004 0,5
№1.005 5.
Пошаговое объяснение:
№1.004
По действиям:
1)2,7-0,8=1,9;
2)1,9 * 2 и 1/3=
=1 и 9/10 * 2 и 1/3=
перевести в неправильную дробь:
=19/10 * 7/3=
=(19*7)/(10*3)=
=133/30; - числитель первой дроби
3)5,2-1,4=3,8;
4)3,8 : 3/70=
=3 и 4/5 : 3/70=
=19/5 : 3/70=
=(19*70)/(5*3)=
=266/3; - знаменатель первой дроби
5)133/30 : 266/3=
=(133*3)/(30*266)=
=1/20; - результат действий в скобках
6)0,125=1/8
1/20+1/8=7/40;
7)7/40 : 2 и 1/2=
=7/40 : 5/2=
=(7*2)/(40*5)=
=7/100=0,07;
8)0,07+0,43=0,5.
№1.005
По действиям:
1)2 и 3/4 : 1,1=
=2 и 3/4 : 1 и 1/10=
перевести в неправильную дробь:
=11/4 : 11/10=
=(11*10)/(4*11)=
=10/4=5/2;
2)5/2 + 3 и 1/3=
=5/2 + 10/3=
=(15+20)/6=
=35/6; числитель первой дроби.
3)0,4 * 3 и 1/3=
=2/5 * 10/3=
=(2*10)/(5*3)=
=4/3;
4)2,5-4/3=
=2 и 1/2 - 4/3=
=5/2 - 4/3=
=(15-8)/6=
=7/6; знаменатель первой дроби.
5)35/6 : 7/6=
=(35*6)/(6*7)=
=5;
6)5 : 5/7=
=(5*7)/5=
=7; итог перед вычитанием
7)2 и 1/6 + 4,5=
=2 и 1/6 + 4 и 1/2=
=6 и 2/3=20/3;
8)0,375=3/8
20/3 * 3/8=
=(20*3)/(3*8)=
=10/4=5/2; числитель второй дроби
9)2,75 - 1 и 1/2=
=2,75 - 1,5=
=1,25; знаменатель второй дроби
10)5/2 : 1,25=
=5/2 : 1 и 1/4=
=5/2 : 5/4=
=(5*4)/(2*5)=
=2; итог перед вычитанием
11)7-2=5.
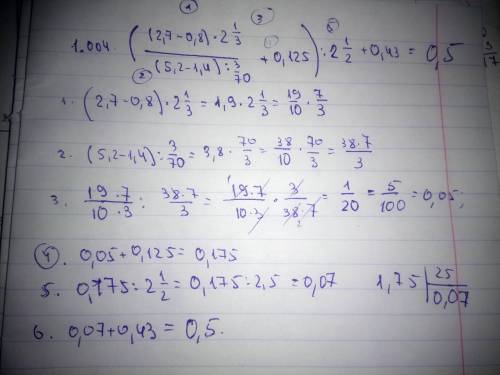
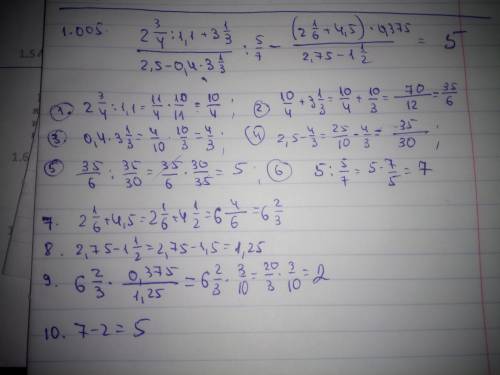
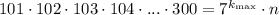
Найдем, сколько чисел от 101 до 300 делятся на 7.
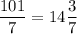
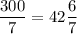
Числа от 101 до 300, делящиеся на 7, дают частные от 15 до 42 включительно. Значит, их количество равно:
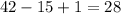
Но, среди чисел от 101 до 300 есть такие, которые делятся на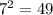 
. Найдем их количество.
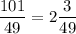
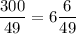
Числа от 101 до 300, делящиеся на 49, дают частные от 3 до 6 включительно. Значит, их количество равно:
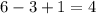
Среди чисел от 101 до 300 делящихся на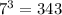 
, а также на большие степени числа 7 нет.
Значит, 28 чисел имеют сомножитель "7". Кроме этого 4 числа имеют еще один сомножитель "7". Значит, всего сомножителей "7" имеется:
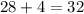
ответ: 32
2<6x
1<3x
x>1/3
решение x∈ (1/3;+∞)
значит не является решением x∈(-∞;1/3)