S= 200 га;
t1= планируемое время посадки;
t2= реальное время посадки;
т.е. t2= x, t1= x+2
V1= планируемая скорость посадки;
V2= реальная скорость посадки;
т.е. V2= V1+5
найдём t2:
t1= S/V1; V1= S/t1; V1= S/x+2; V1= 200/x+2.
t2= S/V2; V2= S/t2; V2= S/x; V2=200/x.
V2= V1+5, откуда V1= V2-5= (200/x)-5.
200/x+2 = (200/x)-5 ,умножим всё это на "x(x+2)"
200x = 200(x+2)-5x(x+2)
200x+400-5x2-10x-200x=0
-5x2-10x+400=0
x2+2x-80=0
Решить по теореме Виета.
ответ: 8 дней
Пошаговое объяснение:
1. Первый изготовил за день x−8 (деталей), второй — х (деталей), третий — x−8+x−44 = 2x−52 (деталей). Всего изготовили за день 84 деталей. Составим и решим уравнение:
x−8+x+2x−52 = 84
4x = 144
x = 36
Первый изготовил за день x−8 = 36−8 = 28 деталей;
третий изготовил за день 2x−52 = 36·2−52 = 20 деталей.
Внеся рационализаторские изменения:
первый стал обтачивать 28+3 = 31 деталей в день;
третий стал обтачивать 20+6 = 26 деталей в день.
Первый рабочий стал обтачивать 31·25 = 775 деталей в месяц;
третий рабочий стал обтачивать 26·25 = 650 деталей в месяц.
ответ: Первый рабочий — 775 деталей, третий рабочий — 650 деталей.
2. В этом задании два варианта ответа, в зависимости, какое из чисел на что делить.
1-й вариант
Обозначим первое число за x, тогда второе за x+288. Поделим первое на 3, тогда второе на 15. Составим и решим уравнение:
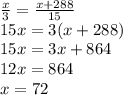
Первой число: x = 72;
второе число: x+288 = 72+288 = 360.
ответ: 72, 360.
2-й вариант
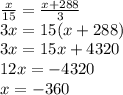
Первой число: x = −360;
второе число: x+288 = −360+288 = −72.
ответ: −72, −360.
1/a - a^2b^2/72 - b^2
72-a^3b^2-72ab^2 / 72a
При a=6,5 , b=0,7 , 72-a^3b^2-72ab^2 / 72a = 72-6,5^3*0,7^2-72*6,5*0,7^2 / 72*6,5 = 72 - 6,5^3*(7/10)^2-72*13/2*(7/10)^2 / 468 = 72-6,5^3* 49/100 -36*13* 49/100 / 468 = 72- 49*6,5^3/100 - 9*13*49/25 / 468 = 72- 49*(13/2)^3 /100 - 5733/25 / 468 = 72- 49* 13^3/2^3 /100 - 5733/25 /468 = 72- 49*13^3 /800 - 5733/25 / 468 = - 3933/25 - 49*13^3 /800 /468 = - 125856+49*13^3 /800 /468 = - 125856+49*13^3 /374400 = - 125856+49*2197 /374400 = -125856+107653 /374400 = - 233509/374400 ~(приблизительно) -0,623689