из этого стиха можете подобрать себе рисунок
Мы гуляли в зоопарке.
Было лето, очень жарко.
Солнце по небу гуляло
И на блин похожим стало.
И все звери стали тоже
На кого-то вдруг похожи.
Слон - на папин пылесос,
Страус - на большой насос,
Черепаха - на машинку,
Со своею твердой спинкой.
А сова - узнал я сразу-
Как большая наша ваза.
На спираль похож баран,
А жираф - подъёмный кран,
Хвост павлина - мамин веер,
Соловей поёт как плеер,
Даже утка, мне казалось,
На утюг похожей стала.
А змея в живой природе
Словно шланг на огороде.
Обезьянка корчит рожи
На кого ж она похожа?
Думал-думал я полдня,
И придумал - на меня!
Пусть х - это первое число, а у - второе число, тогда
х+у=3(х-у) это означает что сумма двух чисел втрое больше их разности
2(х+у)=ху - это означает что сумма двух чисел вдвое меньше их произведения
Теперь составляем систему из этих 2х уравнений и решаем ее.
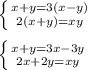
Из первого уравнения выражаем х, получаем:
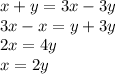
Подставляем во второе уравнение и получаем:
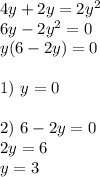
Получили что y=0 или y=3
у=0 не подходит, потому что тогда х=0 и сумма их будет равна 0, и разность тоже равна 0, а значит сумма не будет в 3 раза больше разности
Зато подходит у=3, чтобы найти х надо подставить в уравнение, которое у нас получилось для х,
х=2у=2*3=6
Получили: х=6, у=3
Проверили, оказалось, что 6+3=9, 6-3=3, да, сумма в 3 раза больше, чем разность
6+3=9, 6*3=18, а произведение в 2 раза больше чем сумма.
ответ: Искомыми числами являются числа 6 и 3
Обозначим - p=0.2 - вероятность 6-осных, и q = 0.8 - 4-хосных.
Тогда полная вероятность события для ЧЕТЫРЕХ вагонов будет по формуле (разложения бинома)
P(A) = (p+q)⁴ = p⁴+4p³q+6p²q²+4pq³+q⁴ = 1.
В этой формуле собраны все варианты событий для четырех попыток.
Здесь словами смысл, а цифры даны в приложении.
p⁴ - все четыре 6 осей.
4p³q - три по 6 и один 4.
6p²q² - два по 6 ит два по 4
4pq³ - один 6 и три по 4
q⁴ - все четыре по 4.
В нашей задаче вопрос - три по 6 и один по 4 и это будет
P(A) = 4*p³*q = 0.0256 ≈ 2.56% - ОТВЕТ
ДОПОЛНИТЕЛЬНО
По таблице из приложения можно найти все возможные варианты задач для четырех независимых (случайных) событий.