ответ:
таким же вопросом, на огэ можно проносить только не программированные калькуляторы, a esli vnytrennosti programirovannogo zasymyt' v korpys obychnogo, to dymaiu dolgno srabotat'
p.s. пишу таким шрифтом потому что за nami sledit
p.s.s можно найти список калькуляторов которые можно приносить на экзамен
p.s.s.s если экзамен по , то можно обвернуть калькулятор пленкой перевернуть и залить растопленным шоколадом чтобы было похоже на настоящий, получается когда ты перевернешь плитку шоколада увидишь табло калькулятора
списки калькуляторов которые можно приносить на экзамен указаны здесь:
Сравниваем запись в десятичной и двоичной системе.
1111₁₀ = 1*10³ + 1*10² + 1*10¹ + 1*10⁰ = 10000 + 1000 + 100 + 10 + 1
1111₂ = 1*2³ + 1*2² + 1*2¹ + 1*2⁰ = 8 + 4 + 2 + 1 = 15₁₀.
Видим, что для записи двузначного десятичного числа 15 понадобилось четыре разряда в двоичной системе.
Примеры записи чисел: 10₂ = 1*2¹+ 0*2⁰ = 2₁₀ и 100₂ = 1*2² + 0*2¹ + 0*2⁰ = 4₁₀ и
101₂ = 1*2² + 1*2⁰ = 4 + 1 = 5₁₀ и 110₂ = 2² + 2¹ = 4 + 2 = 6₁₀ и 1110₂ = 2³+2²+2¹ = 8 + 4 + 2 = 14₁₀
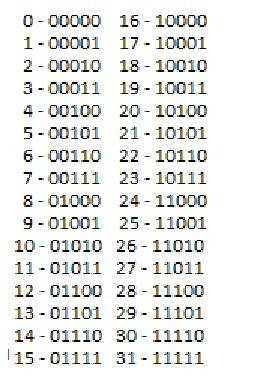
На рисунке в приложении показана запись натуральных чисел от 0 до 31 в двоичной системе исчисления.
В чём же преимущество двоичной системы - в её простоте. В каждом разряде всего два значения - 0 и 1. Недостаток - большое число разрядов для записи числа. Но эту проблему легко решают современные процессоры. Каждый разряд в двоичной системе называется - бит. Число в 32 бит (это 32 единицы в записи) соответствует десятичному числу = 4 294 967 296 , а процессоры в 64 бит могут работать с числами до 1,8*10¹⁹ (19 нулей после запятой). Всего две цифры открывают безграничные возможности.
а)24-8=16ч.
б)24-10=14ч.
в)24-12=12ч.
333.
а)6+2=8кг
б)6+3=9кг.
в)6+4=10кг.
334.
15+21=36
36:2=18-марок каждому
6+9=15
15:2=7.5-число дробное, не удовлетворяет условию задачи,значит не имеет смысла
335.
а) P=2*(a+b)
a=85
b=47
P=2*(85+47)=264м
б)а=х
b=47
P=2*(47+x)=2x+94м
в)a=85
b=x
P=2(85+x)=2x+170м
г)
a=yм
b=xм
P=2(x+Y)=2x+2y(м)