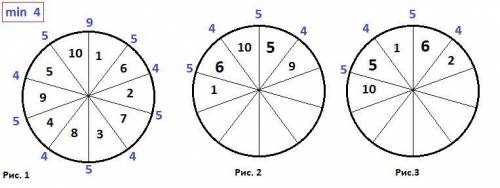
4 - наибольшее возможное значение величины, равной наименьшей из разностей между номерами соседних (по кругу) секторов. Один из вариантов расположения номеров секторов на рис.1.
5 и более получить невозможно, так как для числа 5 с одной стороны можно расположить сектор с номером 10 (10-5=5), а с другой стороны получить разность, более 4, нельзя, так как 5-1=4 и 9-5=4.
Аналогично для числа 6. Если с одной стороны можно получить разность 6-1=5, то с другой стороны более 4 не получится, так как 10-6=4 и 6-2=4. Рис.2 и рис.3
ну вроде так
Пошаговое объяснение:
AB=c; BC=a; CA=b
1) Известная формула для длины биссектрисы, благодаря тому, что угол B = 120 градусов, дает
2) По свойству биссектрисы . Но и BD - биссектриса (пояснение: CD=x; DA=y; x:y=a:c; x+y=b, отсюда выражаем x).
3)
Следовательно, DE - биссектриса угла BDC. Аналогично, DM - биссектриса угла ADB. Поскольку эти углы смежные, угол между их биссектрисами равен 90 градусов:
4) Пусть DE и CM пересекаются в точке F; поскольку они являются биссектрисами треугольника BDC, BF является третьей биссектрисой этого треугольника, а поскольку угол DBC равен 60 градусов, угол DBF равен 30 градусов, а тогда угол ABF равен 90 градусов.
5) Таким образом, в четырехугольнике BMDF углы B и D - прямые, их сумма равна 180 градусов, а тогда вокруг этого четырехугольника можно описать окружность.
6) Остается заметить, что углы DMF и DBF вписаны в эту окружность и опираются на одну дугу; следовательно, они равны. Но угол DBF равен 30, значит, и угол DMF=углу DMO = 30 градусов
4/Задание № 4:
В коробке лежат шарики красного, жёлтого, зелёного и синего цвета. Шариков каждого цвета разное число, не менее 1 и не более 9. Синих, жёлтых и зелёных вместе - 23, а красных, синих и зелёных вместе - 24. Сколько красных шариков?
РЕШЕНИЕ: Так как синих, жёлтых и зелёных шариков - 23, а синих, красных и зелёных - 24, то желтых шариков на 1 меньше, чем красных.
Заметим, что 24 - это сумма трех наибольших возможных значений 9+8+7=24. Значит, красных шариков 7, 8 или 9.
Если красных шариков 9, то желтых - 8, но 8 шариков уже есть - синих или зелёных - не может быть.
Если красных шариков 8, то желтых - 7, но 7 шариков уже есть - синих или зелёных - не может быть.
Если красных шариков 7, то желтых – 6 – все сходится.
ОТВЕТ: 7 шариков