это решение системы
х²-5х+6>0; х²-5х+6=0; по теореме, обратной теореме ВИЕТА, находим корни уравнения х=2;х=3, значит, х²-5х+6=(х-2)(х-3), тогда
(х-2)(х-3)>0
(2-x)/(x-3)≥0⇒(x-2)/(x-3)≤0
второе неравенство равносильно системе
(x-2)(x-3)≤0;
х≠3
Т.о., для решения вопроса области определения данной функции надо решить такую систему
(х-2)(х-3)>0
(x-2)(x-3)≤0;
х≠3
как видим, одновременно произведение (х-2)(х-3) и быть большим или равным нулю и быть меньшим нуля при х≠3, быть не может. поэтому данная функция не определена ни при каких значениях х.
Что мы будем использовать: последовательность 
монотонно возрастает и имеет конечный предел; этот предел обозначается буквой e. Первые цифры числа e все знают. Для нас достаточно знать, что
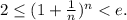
1) 
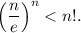При n=1 неравенство очевидно. Предположим, что оно справедливо при некотором n, и докажем, что тогда оно справедливо при n+1. Итак, нужно доказать, что 
Имеем:
2) 
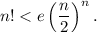При n=1 неравенство очевидно. Предположив, что при некотором n неравенство справедливо, докажем, что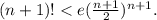 
Имеем:
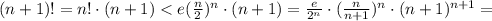
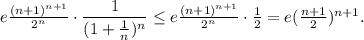
Доказательство завершено благодаря тому, что все натуральные числа расположены "по порядку" одно за другим, и есть первое натуральное число (принцип домино: если доминошки расположить на боку одну рядом с другой на небольшом расстоянии друг от друга в виде змеи, и уронить первую доминошку на вторую, то вторая упадет на третью, третья на четвертую и так далее, пока не упадут все).
4/Задание № 4:
В коробке лежат шарики красного, жёлтого, зелёного и синего цвета. Шариков каждого цвета разное число, не менее 1 и не более 9. Синих, жёлтых и зелёных вместе - 23, а красных, синих и зелёных вместе - 24. Сколько красных шариков?
РЕШЕНИЕ: Так как синих, жёлтых и зелёных шариков - 23, а синих, красных и зелёных - 24, то желтых шариков на 1 меньше, чем красных.
Заметим, что 24 - это сумма трех наибольших возможных значений 9+8+7=24. Значит, красных шариков 7, 8 или 9.
Если красных шариков 9, то желтых - 8, но 8 шариков уже есть - синих или зелёных - не может быть.
Если красных шариков 8, то желтых - 7, но 7 шариков уже есть - синих или зелёных - не может быть.
Если красных шариков 7, то желтых – 6 – все сходится.
ОТВЕТ: 7 шариков