6/Задание № 1:
Сколько чётных шестизначных чисел, делящихся на 15, сумма цифр которых не более 4?
РЕШЕНИЕ: Так как число четное, то оно делится на 2. Кроме этого, так как число делится на 15, то оно делится на 3 и на 5. То есть число оканчивается нулем, и сумма его цифр делится на 3.
Очевидно, что сумма цифр не может равняться нулю. Кроме этого, если сумма цифр не более 4, то единственный допустимый вариант того, чтобы она делилась на 3 - это сумма 3.
Варианты: 300000, 210000, 201000, 200100, 200010, 120000, 102000, 100200, 100020, 111000, 110100, 110010, 101100, 101010, 100110.
ОТВЕТ: 15 чисел
№ 1
Примем объем заказа за 1,
тогда за один час работы первый мастер выполняет 1/12 часть заказа,
а второй мастер - 1/15 часть заказа.
Работая совместно за один час работы мастера выполнят:
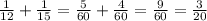 - всего заказа.
- всего заказа.
Весь заказ- 100%.
Найдем процент выполненного заказа за один час совместной работы мастеров:
100% : 20 * 3 = 15%
Значит, не больше 15% заказа мастера выполнят за 1 час совместной работы.
ответ: нет.
№ 2
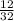
Сократим данную дроб.
Наибольший общий делитель НОД (12; 32) = 4
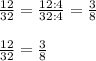
ответ: В 3/8.
№ 4

Приведём данную дробь к знаменателю 18:
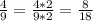
Дроби 17/18 и 11/18 не подходят, так как больше дроби 8/18.
Дроби 1/3 и 2/3 приведём к дробям со знаменателем 9:
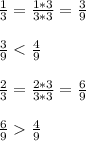
ответ: В 1/3.
Пошаговое объяснение:
№1. 1) первый мастер за 1 час выполнит 1/12 часть работы
второй за 1 час выполнит 1/15 часть работы
1/12 + 1/15 = 5/60 + 4/60 = 9/60 = 3/20 - часть работы выполненная двумя мастерами за 1 час
2) вся работа = 1,
1 : 3/20 = 6 2/3 часа - оба мастера выполнят всю работу, т.е. 100%
3) составим пропорцию: 6 2/3 : 100% = х : 15%, где х - время на 15%,
х = 6 2/3 · 15 : 100 = 1 час. Значит за 1 час они выполнят только 15% работы.
Т.о. для выполнения более 15% работы необходимо больше времени.
ответ: нет
№2. 12/32 = 3/8, сократили числитель и знаменатель на 4. ответ: В
№3. 4/9 = 8/18 , также 2/3 = 12/18, 1/3 = 6/18 . Получили 6 меньше 8, следовательно 1/3 меньше 4/9
или можно просто 1/3 = 3/9, а 3 меньше 4.
ответ: В
Поэтому эти числа делятся на 10, т.к. 10 = 2*5 и 2 и 5 - взаимно простые.
Поэтому эти числа оканчиваются на 0.
Кроме того, по признаку делимости на 3, сумма цифр этих чисел делится на 3, и эта сумма меньше 4 по условию.
Поэтому сумма цифр этих чисел и равна S = 3, поскольку 1, 2, не делятся на 3. Нулю сумма цифр также равняться не может, поскольку числа шестизначные - это значит, что старший разряд не нулевой.
Теперь рассмотрим следующие случаи.
1) Цифры числа, составляющие сумму, - это три единицы.
На первом месте должно быть ненулевая цифра, то есть 1.
1_ _ _ _0
Остальные две единицы можно распределить по четырем пустым местам, а после этого оставшиеся два места заполнить нулями. Найти все такие варианты.
111000;
110100;
110010;
101100;
101010;
100110.
Всего 6 чисел.
2) Цифры числа - это 2 и 1, которые в сумме дают 3.
На первом месте должно быть ненулевое число, то есть 2 или 1.
2.1)
2_ _ _ _ 0,
единицу при этом можно поместить на любое из четырех пустых мест.
Здесь 4 числа.
2.2)
1_ _ _ _ 0,
двойку при этом можно поместить на любое из четырех пустых мест.
Здесь 4 числа.
3) Сумма состоит из единственной цифры = 3.
Очевидно, что эта тройка должна стоять в старшем разряде, поскольку число должно быть шестизначным.
300000.
Одно число.
Теперь считаем количество чисел во всех случаях:
6+4+4+1 = 15.
ответ. 15 чисел.