Пошаговое объяснение:
Нужно найти апофему:
рассмотрим прямоугольный треугольник состощий из части из половины основания(т.к правильная пирамида) высоты и апофемы. Т.к боковая грань образует с основанием 45 градусов, а это значит у нашего прямоугольного треугольника угол между апофемой и половиной основания тоже 45 градусов. Значит это прямоугольный - равнобедренный треугольник, где апофема и гипотенуза и основание. Значит половина основания =18
Следовательно длина основания =36 (она же сторона нашего квадрата-основания(тк пирамида правильная))
А длина апофемы из теоремы пифагора а=
=18
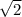
Значит площадь основания So=36*36=1296
А площадь боковой поверхности Sб=4S(треугольника)
треугольник у нас образуют 2 грани и сторона квадрата - основания, апофема высота этого треугольника S(треугольника)=1/2*18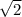*36=324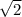
Sб=4*324*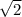=1296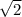
S пов =1296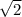+1296=3128,8
Обьем пирамиды
V=1/3*So*h
V=1/3*1296*18=7776
Пошаговое объяснение:
Система уравнений:
b₁+b₄=-49; b₁+b₁q³=-49; b₁(1+q³)=-49; b₁=-49/((1+q)(1-q+q²))
b₂+b₃=14; b₁q+b₁q²=14; b₁(q+q²)=14; b₁=14/(q(1+q))
-49/((1+q)(1-q+q²))=14/(q(1+q)) ×((1+q)/7)
-7/(1-q+q²)=2/q
-7q=2-2q+2q²
2q²-2q+7q+2=0
2q²+5q+2=0; D=25-16=9
q₁=(-5-3)/4=-2 - знаменатель геометрической прогрессии.
b₁(1+(-2)³)=-49; b₁=-49/-7=7- 1-й член геометрической прогрессии.
q₂=(-5+3)/4=-1/2 - знаменатель геометрической прогрессии.
b₁(1+(-1/2)³)=-49; b₁=-49·8/7=-56- 1-й член геометрической прогрессии.
ответ: b₁=7; q=-2 и b₁=-56; q=-1/2.
а) 5/46 + 7/69 + 1/3;
5 : 46 = 0,1;
7 : 69 = 0,1;
1 : 3 = 0,3;
0,1 + 0,1 = 0,2;
0,2 + 0,3 = 0,5
5/46 + 7/69 + 1/3 = 5/10.
б) 121/350 - 47/140;
121 : 350 = 0,34;
47 : 140 = 0,33;
0,34 - 0,33 = 0,01.
121/350 - 47/140 = 1/100.
в) 31/48 + 17/40 - 7/16;
31 : 48 = 0,64;
17 : 40 = 0,42;
7 : 16 = 0,43;
0,64 + 0,42 = 1,06;
1,06 - 0,43 = 0,63.
31/48 + 17/40 - 7/16 = 63/100.