ответ:Масса всех овощей равна - 7.92 кг.
Масса овощей во второй корзине - на 20 % меньше.
Определим массу овощей в каждой корзине.
Обозначим массу овощей в первой корзине через х. Определим буквенное значение массы овощей во второй корзине.
100 - 20 = 80 %.
Х * 0,8 = 0,8х.
Х + 0,8х = 1,8х.
Составим выражение.
1,8х = 7,92.
Х = 7,92/1,8 = 4,4.
Следовательно, масса овощей в первой корзине равна 4,4.
Определим массу овощей во второй корзине.
7,92 - 4,4 = 3,52.
ответ: масса овощей в первой корзине равна 4,4, масса овощей во второй корзине равна 3,52 кг.
Решение во вложении.
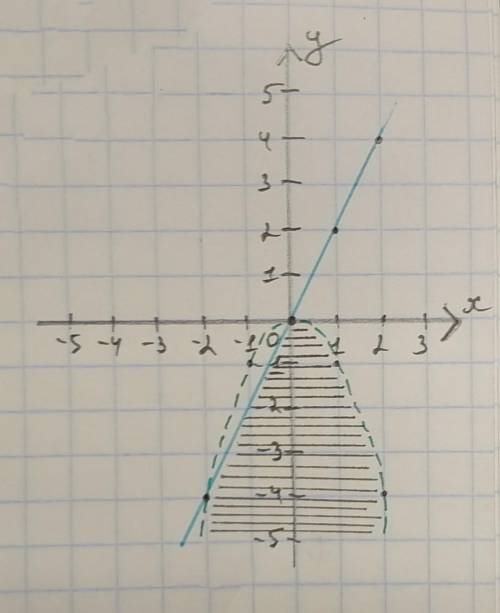
Для решения неравенства грфически вам нужно преобразовать его в функцию f(x)=(...), построить графики данных уравнений, а затем определить, в какой из плоскостей, ограничиваемых графиком, находится нужное множество решений. Для прямой - слева или справа, для параболы - внутри неё или снаружи. Для этого берём любую точку из перечисленных областей и подставляем в неравенство. Если оно верное, зашриховываем выбранную зону. Если нет - противоположную ей область. Для прямой это оказалась область справа от неё, а для параболы - внутри. Затем ищем пересечение штриховок. Это ответ.
Обратите внимание: графическим решением неравенства при строгом знаке (> или <) является ТОЛЬКО определённая вами область, высекаемая графиком. Если знаки нестрогие (<= или >=), то точки самого графика тоже принадлежат множеству решений системы.
Обращаю внимание: я нарисовала новый чертёж с ответом отдельно. Это делать необязательно, достаточно просто хорошо прорисовать область решений на первом чертеже.

2) Нет фото.
3)
а) 1140 кг = 1,140 т
б) 8 см = 0,08 м
4) Сумма двух смежных углов равна 180°
Два угла по 65° и два угла по
180 - 65 = 115°
5)
4/9 = 0,444 и 3/5 = 0,6 и 0,7.
Самое большое - 0,7.
6) С(-3)___D(-1)__A(0)B(5)
AD = AB-BD = 5 - 6 = -1